2. Grade Change Rate

A vehicle enters the curve at g₁ and after a distance of L it departs the curve at g₂. The total grade change is (g₂-g₁). The grade change rate, k, is the total grade change divided by the distance, Equation B-5.

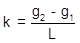Equation B-5

For example, a -2.00% grade into a +1.00% grade connected with a 400.00 ft curve has a k of:

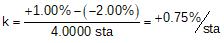
This tells us that the grade changes +0.75% per each 100 ft of curve. If we go 100 ft past the BVC, the curve grade is -1.00%+0.75% = +0.25%

Increasing the curve length to 900.00 ft changes k to +0.33%/sta.

The second smaller k means the longer curve is flatter since is spreads the total grade change over a longer distance, Figure B-4.

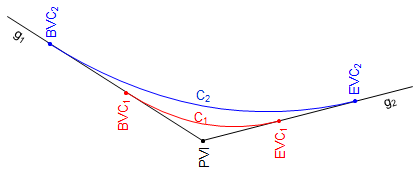Figure B-4 Different Curve Lengths

Note that the example was a sag curve with a positive k: we went from a negative grade to a positive grade. A crest curve, on the other hand, would have a negative grade change rate, Figure B-5.

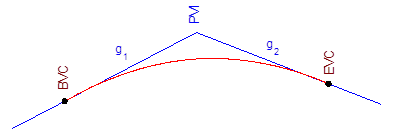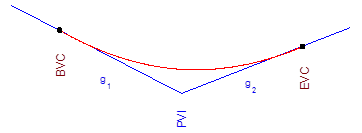Figure B-5 Crest and Sag Curves

What about curves whose grades at both ends are different but have the same mathematical sign? Figure B-6 shows four different curve situations where the incoming and outgoing grades have the same mathematical sign.

Figure B-6 Grades with Same Mathematical Sign

The two curves on the left are both crest curves having a negative k since the outgoing grades are less than the incoming grades.

The two curves on the right are sag curves having a positive k since their outgoing grades are mathematically greater (less negative or more positive) than the incoming grades.