5. The Shortest Distance Between Two Points...

The shortest distance between two points on a(n) __________ is a(n) __________ . 

• plane; straight line
• sphere; circular arc
• ellipsoid; ??

On an ellipsoid:

• If the points are at the same longitude, the distance is an elliptical arc along the meridian.
• if the points are at the same latitude, the distance is a circular arc.
• if the points are not at the same longitude and latitude, the shortest distance is a geodesic.

Take two points A and B on the ellipsoid. Because their normals are in different directions, the elliptical sections between the two points are different, Figure C-13.

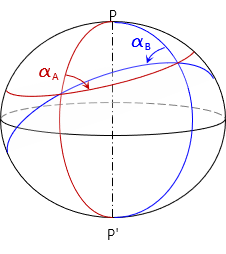Figure C-13 Elliptical Sections

An instrument set at A and sighting at B is actually sighting tangent to the elliptical section in the direction of B'. Similarly, an instrument at B sighting A is sighting A', Figure C-14. These two sight directions are not parallel because of meridian convergence,

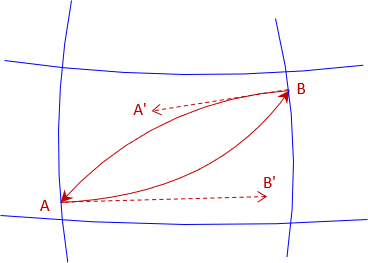Figure C-14 Sightings

The shortest distance from A to B starts tangent to sight A-B' and ends tangent to sight B-A'. This line is an s-shaped reverse curve - the geodesic.

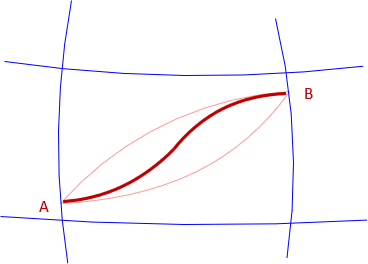Figure C-15 Geodesic

The reverse curvature is most pronounced at directions midway between north-south and east-west.