2. The Ellipsoid

a. Primary Parameters

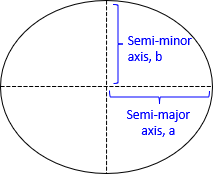
An oblate spheroid, also known as an ellipsoid, begins with an ellipse, Figure C-1. 

Figure C-1 Ellipse

Principle parameters used to define and fix an ellipse are its axes (a & b), flattening (f), first eccentricity (e), and second eccentricity (e').

	Equation C-1
	Equation C-2
	Equation C-3

Fixing any two of the parameters define the rest.

A circle is a special case of an ellipse were a=b. Its flattening and eccentricities are all zero. 

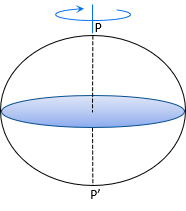
Spinning the ellipse around its semi-minor axis creates a 3D ellipsoid, Figure C-2.

Figure C-2 Ellipsoid

The ellipse is oriented so its semi-minor axis coincides with the Earth's polar axis, P-P'.

Horizontal slices through the ellipsoid are circular sections; vertical ones are elliptical.

 b. Observer's Elements

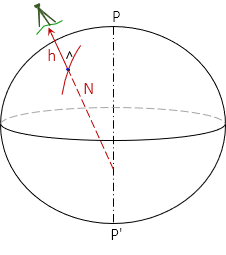
The normal, N, is a line perpendicular to the ellipsoid at the observer's position, Figure C-3. The distance in the normal direction from the ellipsoid to the ground point is the ellipsoidal height, h, also known as the geodetic height. 

Figure C-3 Ellipsoidal Normal

The normal intersects along the ellipsoid minor axis. It terminates at the center only if the observer is at either pole or on the Equator.

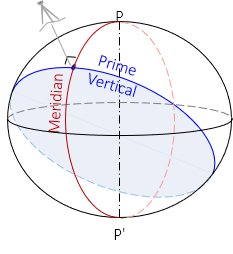
The observer's meridian, Figure C-4, is the elliptical section containing the observer's normal and the semi-minor (polar) axis, P-P'.

Figure C-4 Observer's Meridian

The meridian defines geodetic north at the observer's position. Adjacent meridians converge to the poles P and P'. 

The prime vertical is a circular section perpendicular to the observer's meridian, Figure C-5. Its radius is N and it defines geodetic east at the immediate location. 

Figure C-5 Prime Vertical