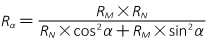4. Radii
A spheroid has a constant radius throughout but an ellipsoid does not. At the equator, the diameter of the ellipsoid is the semi-major axis, a. At the north pole of the same meridian, the radius is the semi-minor axis, b. In between, the meridian is an elliptical arc so its radius doesn't change in linear fashion from Equator to pole.
If you move at an angle to the meridian, you are traveling along another elliptical arc with ever changing radius.
So when we talk about a radius, we have to identify what kind. There are basically three:
- Meridian
- Prime vertical
- Azimuth
a. Meridian
Because the meridian is an elliptical section it does not have a constant radius. The shorter the elliptical arc segment, the closer it comes to being a circular arc. The meridional radius, RM, is the radius of an infinitesimally short arc in the meridian at the observer's position, Figure C-10 an Equation C-13.
 |
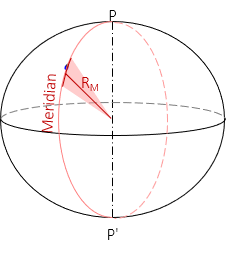| Figure C-10 Radius in the Meridian |
 |
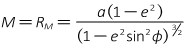Equation C-13 |
b. Prime vertical
The prime vertical is a circular section with the normal as its radius, Figure C-11 and Figure C-14.
 |
| Figure C-11 Radius in the Prime Vertical |
 |
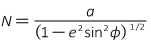Equation C-14 |
Equation C-14 is the same as Equation C-7 because the normal length is used for the Lat/Long <> TRS conversions.
c. Azimuth
A meridian is an ellipse with the same semi-major and -minor axes as the reference ellipsoid. Connecting two points A and B not in the same meridian will create a new ellipse. If the points are at:
- the same latitude, the ellipse will be at a 90° azimuth to A's and B's meridians and form a circle of fixed radius.
- different latitudes, the ellipse will be at an azimuth other than 90° (or 270°) and have semi-major and -minor axes different than the reference ellipsoid.
The radius in the direction of line AB is similar to a meridional radius except it is for a section along the new ellipse, Figure C-12.
 |
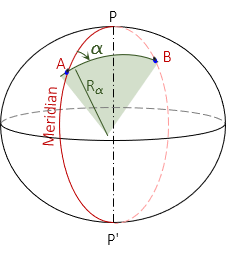| Figure C-12 Radius in an Azimuth |
Either Equation C-15 is used to determine the radius.
 |
Equation C-15 |
d. Comparison
So how different are the radii? For example, let's use:
- Latitude of point A is 41°30'00"
- Azimuth and distance to point B are 55°45'00" N and 10,000.00 ft.
- GRS 80 ellipsoid a = 6,378,137.0 m, e = 0.08181 919104
Radius in the Meridian
Radius in the prime vertical
Radius in the Azimuth
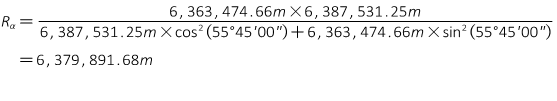
The difference between the largest and smallest is 24,056.59m - seemingly quite a large range, although it's only 0.38%.