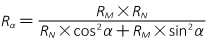Chapter C. Mathematical Surface

1. Background

Point positions can be expressed in relative or absolute terms.

• A relative position is generally a distance and direction from another point. These are typical in smaller scale surveys.
• Absolute positions are angles or distances from a reference system origin. These require a mathematical framework covering larger, even global, areas.

Although we measure on the physical Earth while referenced to the geoid, both of those surfaces are irregular. For small areas measurements can be referenced to a flat plane. With larger projects, however, the Earth's configuration must be accounted for. For this, we need a mathematical model. Since the Earth (and geoid) are flattened at the poles and bulging at the equator, an oblate spheroid fits the bill.

2. The Ellipsoid

a. Primary Parameters

An oblate spheroid, also known as an ellipsoid, begins with an ellipse, Figure C-1. 

Figure C-1 Ellipse

Principle parameters used to define and fix an ellipse are its axes (a & b), flattening (f), first eccentricity (e), and second eccentricity (e').

	Equation C-1
	Equation C-2
	Equation C-3

Fixing any two of the parameters define the rest.

A circle is a special case of an ellipse were a=b. Its flattening and eccentricities are all zero. 

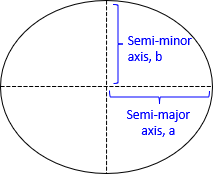
Spinning the ellipse around its semi-minor axis creates a 3D ellipsoid, Figure C-2.

Figure C-2 Ellipsoid

The ellipse is oriented so its semi-minor axis coincides with the Earth's polar axis, P-P'.

Horizontal slices through the ellipsoid are circular sections; vertical ones are elliptical.

 b. Observer's Elements

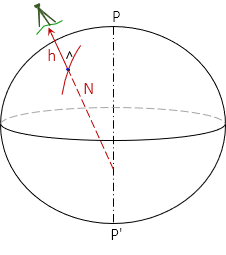
The normal, N, is a line perpendicular to the ellipsoid at the observer's position, Figure C-3. The distance in the normal direction from the ellipsoid to the ground point is the ellipsoidal height, h, also known as the geodetic height. 

Figure C-3 Ellipsoidal Normal

The normal intersects along the ellipsoid minor axis. It terminates at the center only if the observer is at either pole or on the Equator.

The observer's meridian, Figure C-4, is the elliptical section containing the observer's normal and the semi-minor (polar) axis, P-P'.

Figure C-4 Observer's Meridian

The meridian defines geodetic north at the observer's position. Adjacent meridians converge to the poles P and P'. 

The prime vertical is a circular section perpendicular to the observer's meridian, Figure C-5. Its radius is N and it defines geodetic east at the immediate location. 

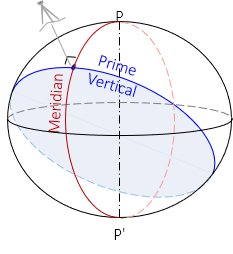Figure C-5 Prime Vertical

3. Spheroidal Coordinates

a. Angular

Around 150 BC, Ptolemy created his first world atlas consisting of twenty-seven pages of maps compiled from observation and traveler's stories. His was the first documented use of east-west and north-south grid lines with positions identified by latitude and longitude. It's a system still used today, albeit with a more accurate representation of the Earth than was possible for Ptolemy.

Latitude and longitude are angular values, one north-south, the other east-west, from two reference planes.

Latitude, Φ, is the angle in the meridian from the Equatorial plane to the normal line at the observer's position. Latitude ranges from 90° South to 90° North (-90° to +90°).

Longitude, λ, is the angle in the Equatorial plane from a reference meridian to the observer's meridian. Longitude varies from 0° to 180° East for the eastern hemisphere; 0° to 180° West for the western hemisphere. Historically the reference meridian used depended in part on the mapmaker's native country - many countries had their own defined by a significant location. Ptolemy's was located in the Canary and Maderia Islands. Others were in Rome, Copenhagen, Jerusalem, Paris, Philadelphia,... Today the Greenwich Meridian is generally used as the 0° longitude line.

On a sphere the normal is radial from the sphere's center, Figure C-6. These latitudes and longitudes are generally referred to as geocentric or geographic coordinates.

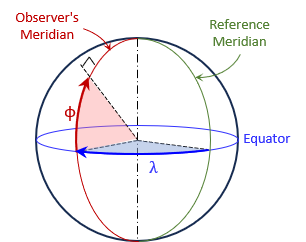Figure C-6 Geographic Coordinates

On an ellipsoid the normal intersects somewhere along the semi-minor axes, Figure C-7. These latitudes and longitudes are geodetic coordinates.

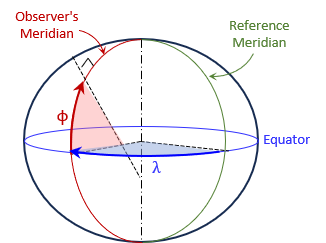Figure C-7 Geodetic Coordinates

While geographic and geodetic coordinates are defined similarly and their values at a point would be very close, they are in fact different. The surveying and mapping community uses geodetic coordinates.

A point's absolute 2D position can be expressed with its latitude and longitude. Its 3D position can be expressed by adding the height abovre the ellipsoid.

b. Linear

Latitude and longitude isn't a convenient system to measure or compute in nor are unit lengths consistent. For example, one degree of longitude at the equator is much longer than one degree at 60° N latitude, and non-existent at 90°N latitude.

An alternative global system is the Terrestrial Reference System (TRS) also known as the Earth-Centered Earth-Fixed (ECEF) system. This is a three-axis linear system with the original at the Earth's mass center, Figure C-8. 

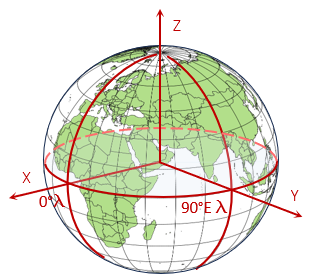Figure C-8 Terrestrial Reference System

The X and Y axes are in the Equatorial plane with X passing through the Greenwich Meridian and Y through 90°E longitude. The Z axis is perpendicular to the Equatorial plane and positive through the North Pole.

A point's 3D position is given by its (X,Y,Z) coordinates.

Although TRS is a linear system, it is not convenient for surveying or mapping applications because of coordinate magnitudes. For example, the coordinates of a control point in southcentral Wisconsin is  21,919.631m X, -4,679,204.603m Y, 4,320,134.562m Z. Their size makes them cumbersome to work with.

Another issue, though less serious, is mapping vertical objects. To map a tall building we generally locate its footprint and assume the upper structure falls within it (unless there are significant protuberances). In the TCS, the top of a building has different coordinates than its bottom. Take for example the TV tower in figure C-9.

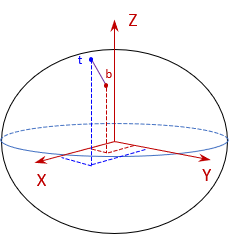Figure C-9 Mapping a Tower in TRS

Although its height is exaggerated, Figure C-9 clearly demonstrates that the top (t) and bottom (b) have different coordinates.

c. Converting coordinates

 Equations C-4, -5, and -6 are used to convert geodetic to TRS coordinates:

	Equation C-4
	Equation C-5
	Equation C-6

 where:

Φ, λ	Point latitude and longitude; west longitude is a negative value.
h	Ellipsoidal height; distance to point from the ellipsoid along the normal.
N	Radius in the prime vertical (discussed in next section)
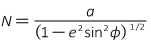		Equation C-7
e	Ellipsoidal eccentricity

Equations C-8 through -12 convert TRS coordinates to geodetic: 

	Equation C-8
	Equation C-9
	Equation C-10
	Equation C-11
	Equation C-12

4. Radii

A spheroid has a constant radius throughout but an ellipsoid does not. At the equator, the diameter of the ellipsoid is the semi-major axis, a. At the north pole of the same meridian, the radius is the semi-minor axis, b. In between, the meridian is an elliptical arc so its radius doesn't change in linear fashion from Equator to pole.

If you move at an angle to the meridian, you are traveling along another elliptical arc with ever changing radius.

So when we talk about a radius, we have to identify what kind. There are basically three:

• Meridian
• Prime vertical
• Azimuth

a. Meridian

Because the meridian is an elliptical section it does not have a constant radius. The shorter the elliptical arc segment, the closer it comes to being a circular arc. The meridional radius, R_M, is the radius of an infinitesimally short arc in the meridian at the observer's position, Figure C-10 an Equation C-13.

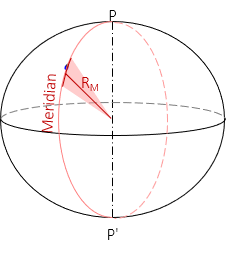Figure C-10 Radius in the Meridian

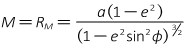Equation C-13

b. Prime vertical

 The prime vertical is a circular section with the normal as its radius, Figure C-11 and Figure C-14.

Figure C-11 Radius in the Prime Vertical

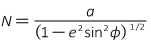Equation C-14

Equation C-14 is the same as Equation C-7 because the normal length is used for the Lat/Long <> TRS conversions.

c. Azimuth

A meridian is an ellipse with the same semi-major and -minor axes as the reference ellipsoid. Connecting two points A and B not in the same meridian will create a new ellipse. If the points are at:

• the same latitude, the ellipse will be at a 90° azimuth to A's and B's meridians and form a circle of fixed radius.
• different latitudes, the ellipse will be at an azimuth other than 90° (or 270°) and have semi-major and -minor axes different than the reference ellipsoid.

The radius in the direction of line AB is similar to a meridional radius except it is for a section along the new ellipse, Figure C-12. 

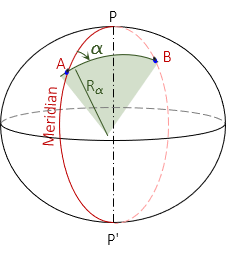Figure C-12 Radius in an Azimuth

Either Equation C-15 is used to determine the radius.

Equation C-15

d. Comparison

So how different are the radii? For example, let's use:

• Latitude of point A is 41°30'00"
• Azimuth and distance to point B are 55°45'00" N and 10,000.00 ft.
• GRS 80 ellipsoid a = 6,378,137.0 m, e = 0.08181 919104

Radius in the Meridian 

Radius in the prime vertical

Radius in the Azimuth

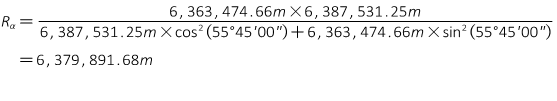
The difference between the largest and smallest is 24,056.59m - seemingly quite a large range, although it's only 0.38%. 

5. The Shortest Distance Between Two Points...

The shortest distance between two points on a(n) __________ is a(n) __________ . 

• plane; straight line
• sphere; circular arc
• ellipsoid; ??

On an ellipsoid:

• If the points are at the same longitude, the distance is an elliptical arc along the meridian.
• if the points are at the same latitude, the distance is a circular arc.
• if the points are not at the same longitude and latitude, the shortest distance is a geodesic.

Take two points A and B on the ellipsoid. Because their normals are in different directions, the elliptical sections between the two points are different, Figure C-13.

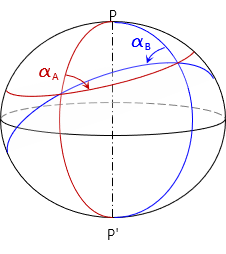Figure C-13 Elliptical Sections

An instrument set at A and sighting at B is actually sighting tangent to the elliptical section in the direction of B'. Similarly, an instrument at B sighting A is sighting A', Figure C-14. These two sight directions are not parallel because of meridian convergence,

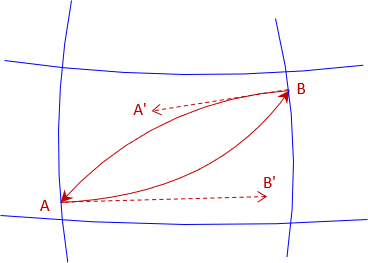Figure C-14 Sightings

The shortest distance from A to B starts tangent to sight A-B' and ends tangent to sight B-A'. This line is an s-shaped reverse curve - the geodesic.

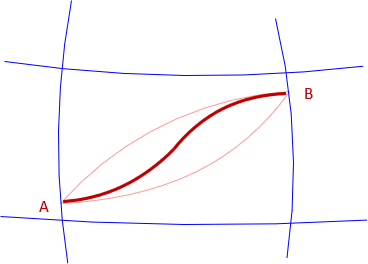Figure C-15 Geodesic

The reverse curvature is most pronounced at directions midway between north-south and east-west.