5. Examples
a. Traverse 1
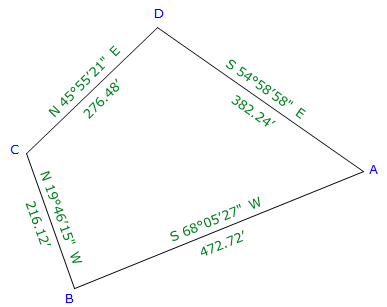
Figure G-11 shows the example Bearing Traverse with the previously computed adjusted Latitudes and Departures.
 |
|
||||||||||||||||||
| Figure G-11 Example DMD Traverse |
|||||||||||||||||||
Step (1) Compute the DMDs
Starting with line AB and use Equation G-4 to computed the DMDs.
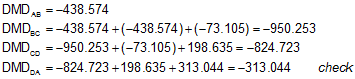
If you examine the Deps and DMDs computations above, you should see a pattern to the computations. This pattern is shown using colored arrows below.

Step (2) Multiply DMDs by Lats; add the products
| Adjusted | ||||
| Line | Lat (ft) | Dep (ft) | DMD (ft) | DMD x Lat (sq ft) |
| AB | -176.386 | -438.574 | -438.574 | +77,358.3 |
| BC | +203.382 | -73.105 | -950.253 | -193,264.4 |
| CD | +192.340 | +198.635 | -824.723 | -158,627.2 |
| DE | -219.336 | +313.044 | -313.044 | +68,661.8 |
|
sum: |
-205,871.5 | |||
Step (3) Compute the area using Equation G-6
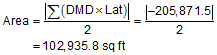
Note that this is the same as computed by coordinates. Surprise.
b. Traverse 2
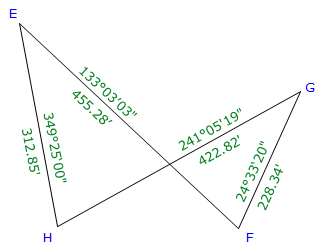
What about the Crossing Traverse?
|
|
|
|
Figure G-12 |
Figure G-13 |
The parcel area, Figure G-12, can not be determined by DMDs without additional computations. By definition, Area by DMDs is limited to travel along the traverse path so you would be determining the area of E-F-G-H-E, Figure G-13. That area doesn't make sense since the traverse crosses itself. To compute the area of the parcel by DMDs, you would need to determine the Lat and Dep of lines EF and FH, then compute DMDs around the perimeter. By the time all that was done, the area could have been computed by coordinates.