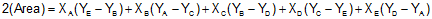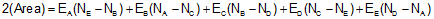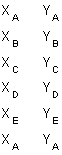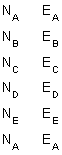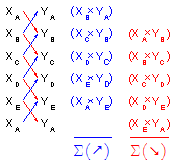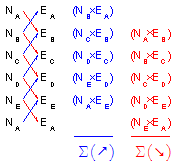2. Area By Coordinates

a. Concept

The area of a closed non-crossing plane polygon can be computed from the coordinates of the polygon's verticies. The area equations, depending on coordinate format used, are shown here as Equations G-1 and G-2

These equations look complex, more so if you expand all the terms. Rather than memorize each equation, it's easier to remember their pattern and determine the area in tabular fashion.

To accurately compute the traverse area:

(1) Select a start point (it doesn't matter where you start)

(2) Going in sequence around the exterior list each coordinate pair vertically, Figure G-5. Direction of travel around the traverse: clockwise or counter-clockwise doesn't matter, nor does coordinate precedence, eg, (X, Y) or (Y, X). 

(3) The first coordinate pair must be repeated at the bottom of the list. In Figure G-5, the surveyor started at point A and then ended on point A.

(4) Cross multiply the coordinates and sum the products, Figure G-6. Arrows indicate "direction" of multiplication.

The units of the cross products are square linear units - if coordinates are in feet, cross products are sq ft.

(5) Using Equation G-3, compute the traverse area.

Sum each column () and ()

The absolute value is used since the area could be negative depending on the combination of direction around the traverse, coordinate precedence (e.g. X,Y vs Y,X), and cross multiplication order. Just as the square root of 4 can be either +2 or -2, so can the area be positive or negative. Because we're generally interested in the magnitude of the answer, we use the absolute value of the area computed.

While at first all this may look confusing, it's actually pretty easy to remember once you do it a few times.