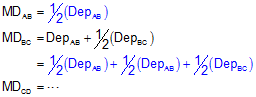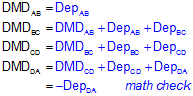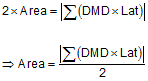4. Area By DMDs

a. Concept

Software uses coordinates for area determination. Most surveyors who solve area manually generally use coordinates also. A traditional method of computing area of a closed polygonal traverse is by DMDs: Double Meridian Distances. While rarely used anymore, every now and then you'll hear it mentioned so we'll spend some time going over Area by DMDs.

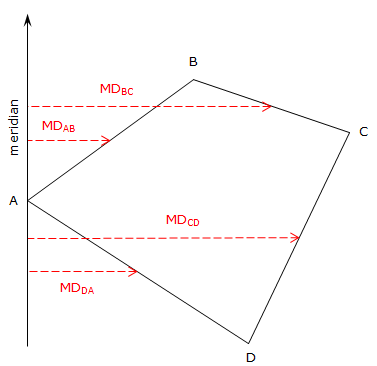
A meridian distance (MD) is the distance from a reference meridian to the center of a line; it is measured in the East (X) direction, Figure G-10.

The reference meridian used can be placed anywhere, but generally, it passes through the first point of the traverse. Triangular and trapezoidal areas can be computed by multiplying a meridian distance by the latitude of the respective line. The base of each triangle or trapezoid coincides with the meridian. Adding the areas, some of which are negative based on the latitude and meridian distance, results in the area of the polygon.

Why then the Double Meridian Distance? Well if we start at point A in Figure G-10 and begin computing meridian distances, we see a pattern start to develop, Equation G-4.

See all those 1/2's? By multiplying both sides of each MD equation by 2, the 1/2's all go away and we're left with Double Meridian Distances (DMDs) on each left side, Equation G-5.

Notice that the DMD of the last line is the same as the Departure of that line except with an opposite math sign. That's the math check.

Multiplying each line's DMD by its Latitude and summing the results will give us double the area.

Just like area by coordinates it looks pretty confusing, but there is a pattern that helps guide the calculations.

You'll sometimes see reference to Area by DPDs (Double Parallel Distance). This is identical to the DMD method except everything is rotated 90°. Parallel distances are determined from an E/W reference line (a parallel) and multiplied by the latitudes.