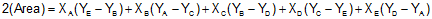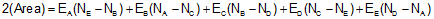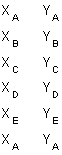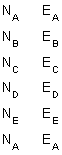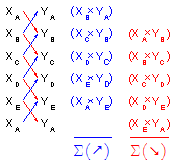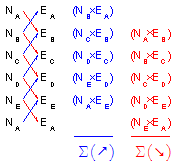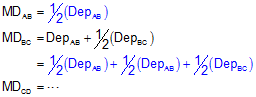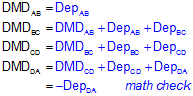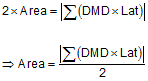G. Area
1. General
Once a loop traverse has been adjusted, how can its area be determined?
 |
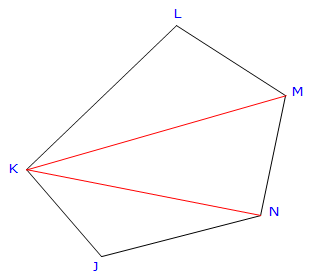
| Figure G-1 Loop Traverse |
We could divide the complex polygon into a series of triangles, compute the area of each triangle, then total them, Figure G-2.
|
|
|
Figure G-2 |
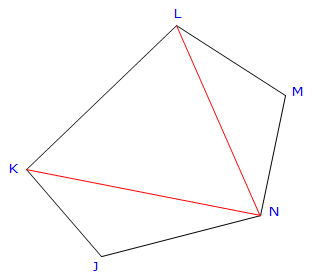
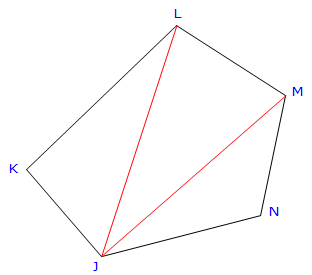
Figure G-3 demonstrates that there can be quite a few possible triangle combinations for a five sided traverse.
|
|
|
Figure G-3 |
To compute a triangle's area, either all three sides or two sides and an included angle are needed. That means additional calculations to obtain distances and/or an angle between lines. In both triangle combinations of Figure G-3, the red lines must be computed by inversing.
The traverse in Figure G-3 is a bit simplistic with just five sides. The more traverse points, the more triangles and combinations and more inverse calculations. It can be especially interesting approach with a concave traverse, Figure G-4, having one or more situations where triangle areas should be subtracted instead of added. Just ome more thing to keep track of.
|
|
|
Figure G-4 |
As with other surveying calculations, we need a systematic, repeatable, and reliable approach to determine traverse area.
2. Area By Coordinates
a. Concept
The area of a closed non-crossing plane polygon can be computed from the coordinates of the polygon's verticies. The area equations, depending on coordinate format used, are shown here as Equations G-1 and G-2
|
In terms of X and Y coordinates |
||
|
|
|
Equation G-1 |
|
In terms of N and E coordinates |
||
|
|
Equation G-2 |
|
These equations look complex, more so if you expand all the terms. Rather than memorize each equation, it's easier to remember their pattern and determine the area in tabular fashion.
To accurately compute the traverse area:
(1) Select a start point (it doesn't matter where you start)
(2) Going in sequence around the exterior list each coordinate pair vertically, Figure G-5. Direction of travel around the traverse: clockwise or counter-clockwise doesn't matter, nor does coordinate precedence, eg, (X, Y) or (Y, X).
|
Using X,Y coords |
Using N,E coords |
|
|
|
| Figure G-5 Listing Coordinates in Sequence |
|
(3) The first coordinate pair must be repeated at the bottom of the list. In Figure G-5, the surveyor started at point A and then ended on point A.
(4) Cross multiply the coordinates and sum the products, Figure G-6. Arrows indicate "direction" of multiplication.
|
Using X,Y coords |
Using N,E coords |
|
|
|
| Figure G-6 Coordinate Cross Multiplication |
|
The units of the cross products are square linear units - if coordinates are in feet, cross products are sq ft.
(5) Using Equation G-3, compute the traverse area.
Sum each column ( ) and (
) and ( )
)
|
|
Equation G-3 |
The absolute value is used since the area could be negative depending on the combination of direction around the traverse, coordinate precedence (e.g. X,Y vs Y,X), and cross multiplication order. Just as the square root of 4 can be either +2 or -2, so can the area be positive or negative. Because we're generally interested in the magnitude of the answer, we use the absolute value of the area computed.
While at first all this may look confusing, it's actually pretty easy to remember once you do it a few times.
3. Examples
Although we carried an additional digit in all previous computations, we'll carry a few more extra here. We'll discuss the area error at the end of the chapter but for now we want to over-compute the area accuracy then report it to an appropriate resolution after we analyze it. If we don't carry additional digits, we could easily increase error due to rounding. To be on the safe side, we'll carry the computations to 0.1 which should be less than the expected error.
a. Example 1
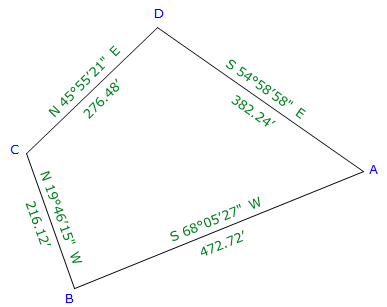
Figure G-7 is a continuation of the Bearing Traverse example we have been using in the past few chapters.
 |
|
|||||||||||||||
| Figure G-7 Example 1 Traverse |
Step (1) Start at point A and going clockwise around the traverse list the coordinates:
|
Point |
N (ft) |
E (ft) |
||
|
A |
500.000 |
2000.000 |
||
|
B |
323.614 |
1561.426 |
||
|
C |
526.996 |
1488.321 |
||
|
D |
719.336 |
1686.956 |
||
|
A |
500.000 |
2000.000 |
remember to return to A | |
Step (2) Cross multiply in one direction:
|
Point |
N (ft) |
E (ft) |
( |
|
|
A |
500.000 |
2000.000 |
647,228.0 |
|
|
B |
323.614 |
1561.426 |
822,865.2 |
|
|
C |
526.996 |
1488.321 |
1,070,602.9 |
|
|
D |
719.336 |
1686.956 |
843,478.0 |
|
|
A |
500.000 |
2000.000 |
|
|
|
|
|
|
|
|
Step (3) Cross multiply in the other direction
|
Point |
N (ft) |
E (ft) |
( |
( ), sq ft ), sq ft |
|
A |
500.000 |
2000.000 |
647,228.0 |
|
|
B |
323.614 |
1561.426 |
822,865.2 |
780,713.0 |
|
C |
526.996 |
1488.321 |
1,070,602.9 |
481,641.5 |
|
D |
719.336 |
1686.956 |
843,478.0 |
889,019.1 |
|
A |
500.000 |
2000.000 |
1,438,672.0 |
Step (4) Add up the columns
|
Point |
N (ft) |
E (ft) |
( |
( |
|
A |
500.000 |
2000.000 |
647,228.0 |
|
|
B |
323.614 |
1561.426 |
822,865.2 |
780,713.0 |
|
C |
526.996 |
1488.321 |
1,070,602.9 |
481,641.5 |
|
D |
719.336 |
1686.956 |
843,478.0 |
889,019.1 |
|
A |
500.000 |
2000.000 |
1,438,672.0 |
|
|
|
|
sums: |
3,384,174.1 |
3,590,045.6 |
Step (5) Using Equation G-3 compute the area
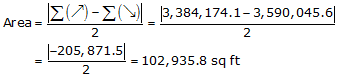
Until we discuss area accuracy more fully, we'll state the area as 102,935.8 sq ft.
There's nothing magical or sacred about point A. We could have stated our list at point C and traveled counter-clockwise around the traverse. As long as we remember to repeat the initial point at the bottom of the list, we will come up with the same area although one could be positive and the other negative.
b. Example 2
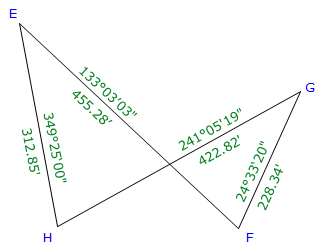
Figure G-8 shows the Crossing Traverse we've been using as another running example.
|
|
|
|||||||||||||||
| Figure G-8 Crossing Traverse |
With a crossing traverse, one must be careful when listing the coordinates. In this case, if you list the coordinates along the original traverse path, E-F-G-H-E, you will be able to compute an area but it will be nonsensical. The traverse turns itself inside out.
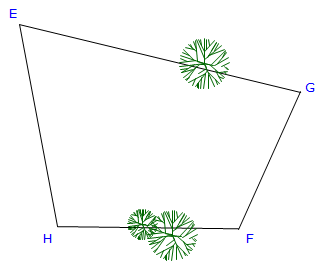
Recall that this survey was on a four-sided parcel having two obstructed lines, Figure G-9.
|
|
|
Figure G-9 |
We want the the area of the parcel, not the traverse.
Step (1) Start at point E and going clockwise around the parcel, list the coordinates.
|
Point |
N (ft) |
E (ft) |
||
|
E |
1000.000 |
200.000 |
||
|
G |
896.890 |
627.584 |
||
|
F |
689.206 |
532.694 |
||
|
H |
692.474 |
257.460 |
||
|
E |
1000.000 |
200.000 |
remember to return to E | |
Step (2)-(4) Cross multiply in both directions; sum the columns.
|
Point |
N (ft) |
E (ft) |
( |
( |
|
E |
1000.000 |
200.000 |
179,378.0 |
|
|
G |
896.890 |
627.584 |
432,534.7 |
624,584.0 |
|
F |
689.206 |
532.694 |
368,876.7 |
477,767.9 |
|
H |
692.474 |
257.460 |
257,460.0 |
177,443.0 |
|
E |
1000.000 |
200.000 |
138,494.8 |
|
|
|
|
|
1,238,252.4 |
1,418,289.7 |
Step (5) Use Equation (G-3) to compute the area
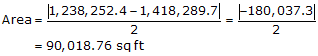
4. Area By DMDs
a. Concept
Software uses coordinates for area determination. Most surveyors who solve area manually generally use coordinates also. A traditional method of computing area of a closed polygonal traverse is by DMDs: Double Meridian Distances. While rarely used anymore, every now and then you'll hear it mentioned so we'll spend some time going over Area by DMDs.
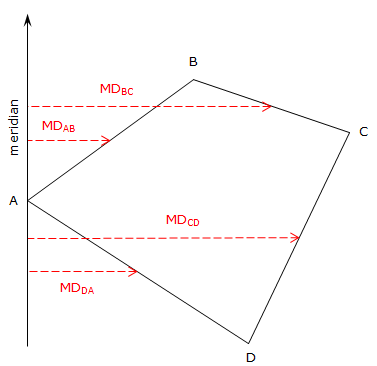
A meridian distance (MD) is the distance from a reference meridian to the center of a line; it is measured in the East (X) direction, Figure G-10.
|
|
|
Figure G-10 |
The reference meridian used can be placed anywhere, but generally, it passes through the first point of the traverse. Triangular and trapezoidal areas can be computed by multiplying a meridian distance by the latitude of the respective line. The base of each triangle or trapezoid coincides with the meridian. Adding the areas, some of which are negative based on the latitude and meridian distance, results in the area of the polygon.
Why then the Double Meridian Distance? Well if we start at point A in Figure G-10 and begin computing meridian distances, we see a pattern start to develop, Equation G-4.
|
|
Equation G-4 |
See all those 1/2's? By multiplying both sides of each MD equation by 2, the 1/2's all go away and we're left with Double Meridian Distances (DMDs) on each left side, Equation G-5.
|
|
Equation G-5 |
Notice that the DMD of the last line is the same as the Departure of that line except with an opposite math sign. That's the math check.
Multiplying each line's DMD by its Latitude and summing the results will give us double the area.
|
|
Equation G-6 |
Just like area by coordinates it looks pretty confusing, but there is a pattern that helps guide the calculations.
You'll sometimes see reference to Area by DPDs (Double Parallel Distance). This is identical to the DMD method except everything is rotated 90°. Parallel distances are determined from an E/W reference line (a parallel) and multiplied by the latitudes.
5. Examples
a. Traverse 1
Figure G-11 shows the example Bearing Traverse with the previously computed adjusted Latitudes and Departures.
 |
|
||||||||||||||||||
| Figure G-11 Example DMD Traverse |
|||||||||||||||||||
Step (1) Compute the DMDs
Starting with line AB and use Equation G-4 to computed the DMDs.
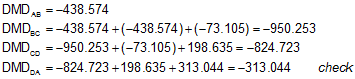
If you examine the Deps and DMDs computations above, you should see a pattern to the computations. This pattern is shown using colored arrows below.

Step (2) Multiply DMDs by Lats; add the products
| Adjusted | ||||
| Line | Lat (ft) | Dep (ft) | DMD (ft) | DMD x Lat (sq ft) |
| AB | -176.386 | -438.574 | -438.574 | +77,358.3 |
| BC | +203.382 | -73.105 | -950.253 | -193,264.4 |
| CD | +192.340 | +198.635 | -824.723 | -158,627.2 |
| DE | -219.336 | +313.044 | -313.044 | +68,661.8 |
|
sum: |
-205,871.5 | |||
Step (3) Compute the area using Equation G-6
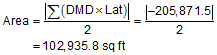
Note that this is the same as computed by coordinates. Surprise.
b. Traverse 2
What about the Crossing Traverse?
|
|
|
|
Figure G-12 |
Figure G-13 |
The parcel area, Figure G-12, can not be determined by DMDs without additional computations. By definition, Area by DMDs is limited to travel along the traverse path so you would be determining the area of E-F-G-H-E, Figure G-13. That area doesn't make sense since the traverse crosses itself. To compute the area of the parcel by DMDs, you would need to determine the Lat and Dep of lines EF and FH, then compute DMDs around the perimeter. By the time all that was done, the area could have been computed by coordinates.
6. Comparison
| Table G-1 | ||
| Method | Advantages | Disadvantages |
|
DMDs |
|
|
|
Coordinates |
|
|
7. Accuracy Revisited
a. How Accurate?
Which method, Coordinates or DMDs, is most accurate? Because both area calculation methods use the same adjusted latitudes and departures, they should have equal accuracy. The best way to determine area accuracy is to propagate all measurement and setup errors into it. Even with a computer that can be a daunting task. If surveying software is available, a sensitivity analysis can be done: vary multiple measurements by introducing reasonable errors into them and examine how the area changes.
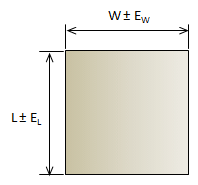
A simplified approach can be used which uses basic error propagation along with the traverse precision. Envision a rectangular parcel which includes the same area as the traverse. Because the area of a rectangle is length times width, the Error of a Product can be used to approximate an accuracy, Figure G-14.
|
|
|
Figure G-14 |
The equation for Error of a Product is:
|
|
Equation G-7 |
in terms of the rectangle:
|
|
Equation G-8 |
EW and EL are the expected errors in the width and length. What do we use for EW and EL? We can approximate the errors using the traverse precision. The precision summarizes up the overall random error effects for that particular traverse. If we multiply a distance by the precision, p, it gives us an expected error in that distance.
|
EL = L x p EW = W x p |
Equations G-9 and G-10 |
Substituting that back into the equation and reducing:
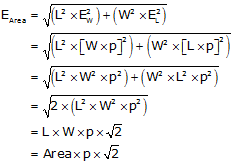
|
Equation G-11 |
This simplified method takes into account the overall quality of the traverse in the form of its precision along with the magnitude of its size.
b. Examples
(1) Bearing Traverse, Figure G-11
Prior to adjustment we determined its precision to be 1/11,900; area computed by coordinates is 102,935.8 sq ft.
Substituting those numbers into Equation G-11:
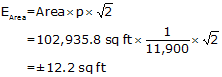
Recall that throughout our calculations, up to that of the area, we carried an additional digit to minimize rounding errors. That means our area uncertainty would be expressed to two sig fig: ±12 sq ft.
The area should be expressed to a level compatible with the uncertainty: 102,936 sq ft.
(2) Crossing Traverse Parcel Survey
Prior to adjustment we determined the Crossing Traverse precision to be 1/10,100. After adjustment its coordinates were used to compute the Parcel's area as 90,018.76 sq ft.
Substituting those numbers into Equation G-11:
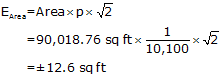
The Parcel's area uncertainty is ±12 sq ft so show it as 90,018 sq ft.
|
|
It happens because of their combination of area and precision that both examples have ±12 sq ft error. Don't assume all areas will have the same error. |
c. A Final Word
We generally have a tendency to overstate area accuracy: it's not uncommon to see a computer generated map with areas expressed to 0.01 sq ft. Surveyors sometimes get caught up in equipment specifications and forget about the propagated errors when multiple measurements are combined. After all, our total station reports distances to 0.01 ft and angles to 01". That should result in an uncertainty smaller than 12 sq ft, shouldn't it?
The area of the square in Figure G-15 on your screen should be 0.01 sq ft; it is 0.1 ft (approx 1.2") on a side (Your browser's magnification and display may affect the square's displayed size. If that's the case, draw a 1.2" square on a piece of paper to visualize it.).
|
|
|
Figure G-15 |
Knowing what we do about how errors occur and accumulate, does it make sense to state an area of 90,018 sq ft to an accuracy of that square?
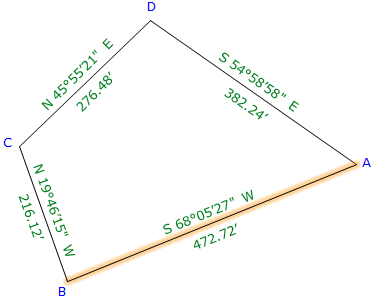
Consider this: How much would the area of the Bearing Traverse example be affected if we offset line AB by 0.01 ft?
|
|
| Figure G-16 Slightly Displacing a Line |
We could approximate the area change with a 0.01' wide by 472.72 ft long rectangle - a difference of about 4.7 sq ft. That 0.01 ft offset would represent relatively small random errors in both lines CB and DA. Instrument and reflector centering errors and measurement errors could easily exceed 0.01 ft error per line. Include pointing errors measuring angles and the potential error can be substantial. Using similar equipment and procedures measuring larger traverses or traverses with more points will also increase the error in the area. So an error of 12 sq ft doesn't seem so bad now, does it?
Using the simplified error propagation, Equation G-10 allows the surveyor to express area to a reasonable level of uncertainty.