G. Area

1. General

Once a loop traverse has been adjusted, how can its area be determined?

Figure G-1 Loop Traverse

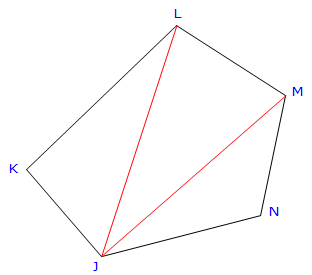
We could divide the complex polygon into a series of triangles, compute the area of each triangle, then total them, Figure G-2.

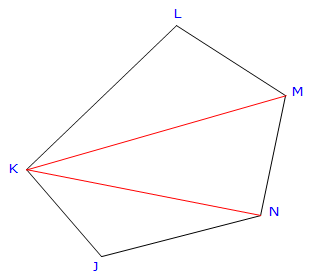
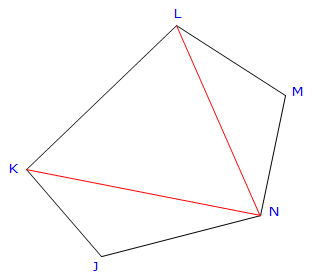
Figure G-3 demonstrates that there can be quite a few possible triangle combinations for a five sided traverse.

To compute a triangle's area, either all three sides or two sides and an included angle are needed. That means additional calculations to obtain distances and/or an angle between lines. In both triangle combinations of Figure G-3, the red lines must be computed by inversing.

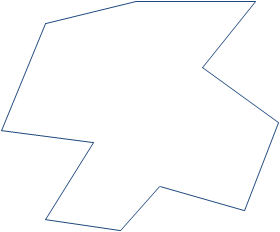
The traverse in Figure G-3 is a bit simplistic with just five sides. The more traverse points, the more triangles and combinations and more inverse calculations. It can be especially interesting approach with a concave traverse, Figure G-4, having one or more situations where triangle areas should be subtracted instead of added. Just ome more thing to keep track of.

As with other surveying calculations, we need a systematic, repeatable, and reliable approach to determine traverse area.