2. Transforming coordinates
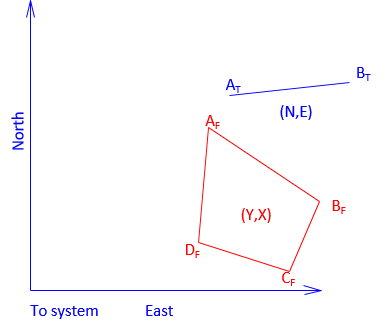
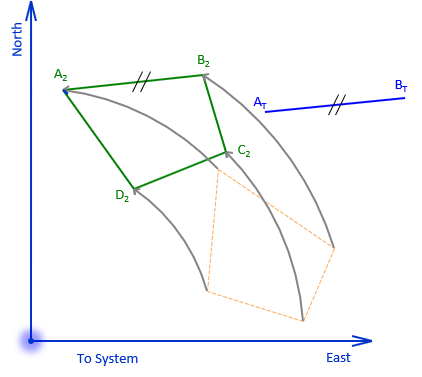
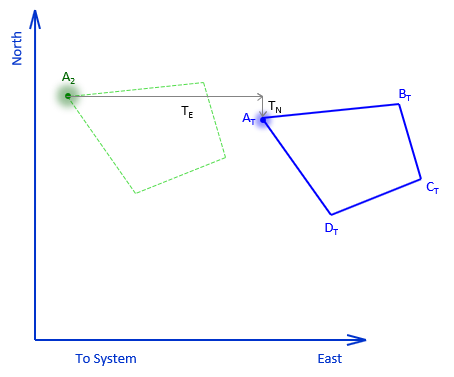
A coordinate transformation changes point positions from one coordinate system to another. It does not require the original measurements used to create the coordinates. Figure J-5 illustrates a situation similar to combining Jones' and Davis' surveys: the same two physical points (A abd B) have two different mathematical positions.
|
|
|
Figure J-5 |
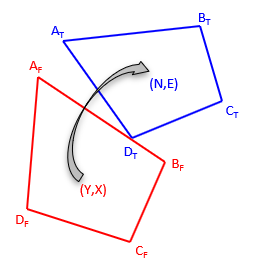
The two coordinate systems are To and From. The To system is final coordinate system in which we'd like all positions expressed. Points AT and BT are the points correctly located in the To system. Points AF and BF are the same points but in a the From system. Points CF and DF are also in the From system and we would like to know their coordinates in the To system.
A transformation consists of three elements
- Scaling
- Rotation
- Translation
We'll discuss the elements in the order shown. To differentiate between the systems we'll used X, Y coordinates for the From system and N, E for the To.
3. Transformation elements
b. Scaling
Scaling is used to increase or decrease distances between the points in order to make them fit in the new system. The distances may be off due to:
- random errors
- systematic errors
- unit conversion (eg, meters to feet)
- ground to grid distortion (in larger regional systems)
- combinations of the above.
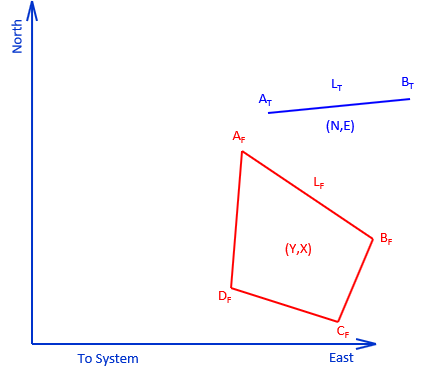
To scale the transformation, we need the length of the same line in both systems, Figure J-16. The length can be from direct measurement (and subsequent adjustment) or by inversing between the coordinates of two common points.
|
|
|
Figure J-6 |
The scale is a ratio between the To and From system line lengths, Equation J-1.
| Equation J-1 | ||
|
LT |
To length |
|
Scaling isn't always necessary depending on the circumstances and allowable error. For example, if a maximum error of 1/20,000 is acceptable, then a scale in the range of 1±1/20,000 (0.99995 to 1.00005) can be treated as 1.00000 and this step skipped.
When accounting for scale there are three approaches:
- Unitary - Maintains a 1:1 relationship between the two coordinate systems.
- Uniform - Enforces the same consistent scale (other than 1) in all directions. Only a single scale is computed for the entire transformation.
Both Unitary and Uniform approaches are referred to as a Conformal Transformation because true shapes are maintained. - Differential - Scale in the North-South direction differs from scale in the East-West direction. Two different scales (SN and SE) are computed for the transformation. This is referred to as an Affine Transformation.
Scale is radially applied from the To system's origin. Once applied another set of updated From coordinates, subscripted 1, are created, Figure J-7.
|
|
|
Figure J-7 |
b. Rotation
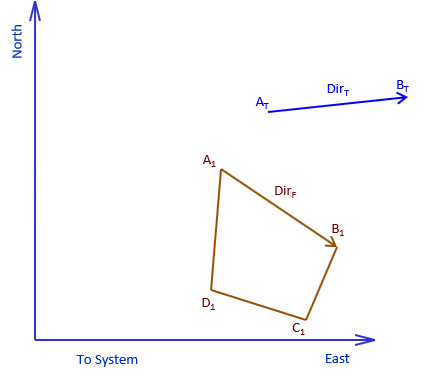
The From coordinates must be rotated to make its directions coincide with those of the To system. To determine the rotation angle we need the direction of a common line in both systems. In Figure J-8, we need to make the direction of line AFBF the same as the direction of line ATBT.
|
|
|
Figure J-8 |
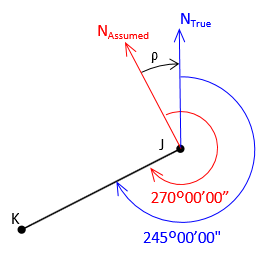
Beacuse a line doesn't physically rotate, we need to make the North meridian of the From system parallel with To's. For example, line JK has an assumed azimuth of 270°00'00"; the same line has a true azimuth pf 245°00'00". The line is the same in both systems, only the directions of North differ, Figure J-9.
|
|
|
Figure J-9 |
The rotation angle, ρ, is the amount the Assumed North must be rotated to coincide with the True North. In this case, it must be rotated clockwise (to the right) by 270°00'00"-245°00'00" = +25°00'00".
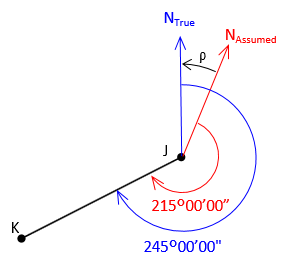
If the Assumed azimuth is 215°00'00" and True azimuth is 245°00'00", Figure J-10, then Assumed North must be rotated counter-clockwise (to the left) which means it must be a negative angle: 215°00'00"-245°00'00" = -30°00'00".
|
|
|
Figure J-10 |
The rotation angle, ρ, is the From direction minus the To direction, Equation J-2.
| Equation J-2 | ||
|
DirT |
To direction | |
|
DirF |
From direction | |
If using two control points, inversing between them in both systems will provide the requisite directions.
The rotation point is the origin of the To coordinate system. The effect of rotating the From meridian creates another updated From coordinate set, sub-scripted 2 in Figure J-11.
|
|
|
Figure J-11 |
c. Translation
The final element consists of two translations: shift positions in the North-South and East-West directions. These are the differences at one point between its To and updated From coordinates, Figure J-12.
|
|
|
Figure J-12 |
Translations are computed from a control point known in both systems. Because the rotation and scale have already been applied, they must be incorporated to determine the translations. The translations are Equations J-3 and J-4 in terms of the original From system.
|
|
Equation J-3 |
|
|
Equation J-4 |
These two final elements complete the transformation, Figure J-13.
|
|
|
Figure J-13 |
e. Transformation Equations
Once the parameters are determined, they are assembled to create the transformation equations, J-5 and J-6, which are used to move other points to the To system, Figure J-14.
|
|
|
| Equation J-6 | |
|
|
|
|
|
Figure J-14 |
f. CAD equivalent
Consider how you would solve this problem in Figure J-3 using CAD. You would use CAD Move, Rotate, and Scale operations, Figure J-15, to put Lot 4 in Lot 3's system. What you've done is apply a coordinate transformation graphically.
|
|
|
Figure J-15 |
g. Number of parameters
A coordinate transformation is sometimes referred to as either a three-, four- or five-parameter transformation. The difference between the number of parameters is how scale is applied. Either way, a certain amount of data (control) is needed in both systems. Each parameter is an unknown which must be solved. This will dictate the minimum amount and type of control that is needed.
| Table J-1 | |||
| Transformation type | Three parameter (Conformal) |
Four Parameter (Conformal) |
Five-Parameter (Affine) |
| Parameters | TN TE ρ |
TN TE ρ S |
TN TE ρ SN SE |
| Scale | Scale = 1 | Single scale in all directions | N/S and E/W scales can differ |
| Control needed in both systems | One point's coordinates, one line's directions |
One point's coordinates, one line's direction, one line's distance |
One point's coordinates, one line's directions, two line's distances |
| or | or | or | |
| two points | two points | two points & one line's directions | |
| or | |||
| three points | |||
These are generally the minimal amounts of control needed to uniquely determine the transformation parameters. For example, a four-parameter transformation has four unknowns. Two control points contribute four knowns: two coordinate pairs. Having only a single control point won't allow you to compute the transformation parameters. At best, you can translate the From coordinates, but there isn't sufficient information to determine a rotation or scale.
Using just the minimum control means errors in the control will be undiscovered and become part of the parameters affecting all points transformed. Additional control data can be used for math checks. Due to the presence of random errors, different combinations of control will result in slightly different transformation parameters. To get a better model which propagates the error into the final positions, all control should be incorporated in a least squares transformation. Creating such a model manually is time consuming so we will not address least squares transformations here. Many surveying software packages usually include an optional least squares transformation.
We will concentrate on the four-parameter model as it works well for most ground-based survey applications. Including a uniform scale absorbs smaller random errors satisfactorily as long as good control is used.