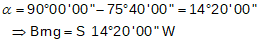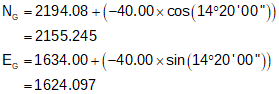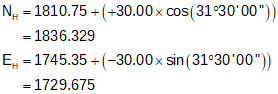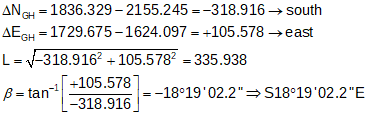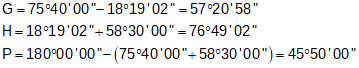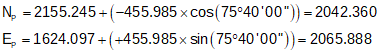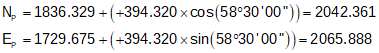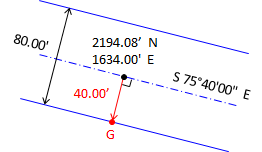
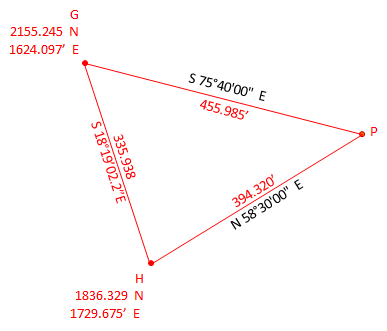
Two intersecting streets are shown on the right. The centerline direction for each is known as are their widths.

Given the coordinates of a point on each centerline, what are the coordinates of the sideline intersection at point P?

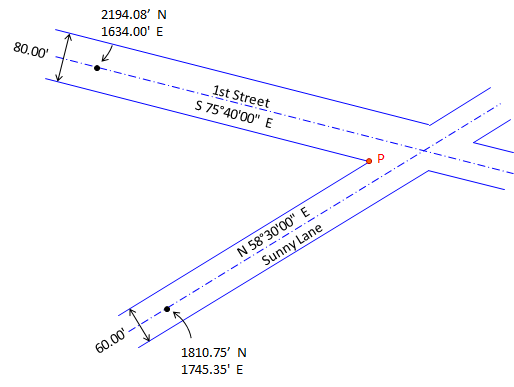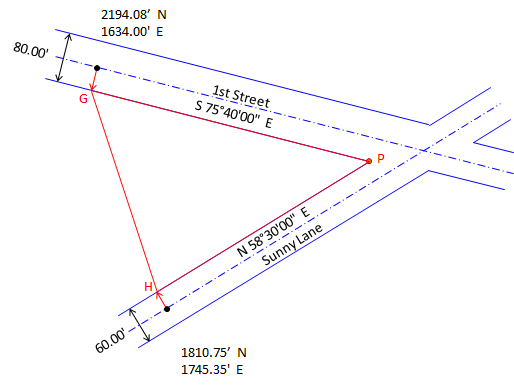Since bearings are given, this is a bearing-bearing intersection.

Because point P is not on the centerlines it should not be connected directly to the two given coordinate points.

Instead, create two new points, G and H, on each sideline. These will serve as the baseline for the intersection triangle.

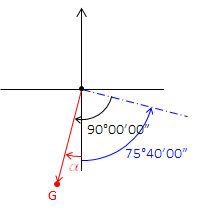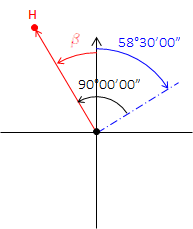
To create point G, go perpendicular to the centerline at the given coordinate:

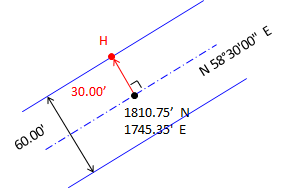
Do the same to create point H:

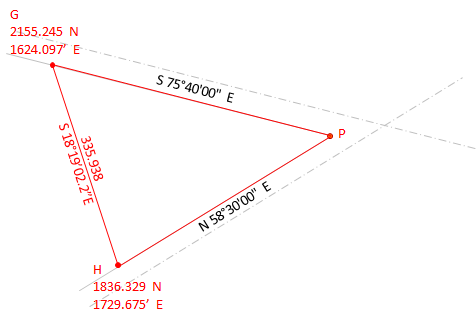Inverse to determine the length and direction of the baseline GH:

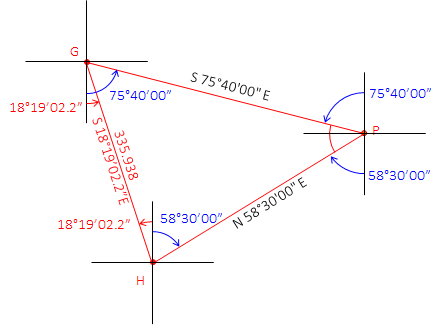Sidelines have the same directions as their respective centerlines. Using those, compute the three angles:

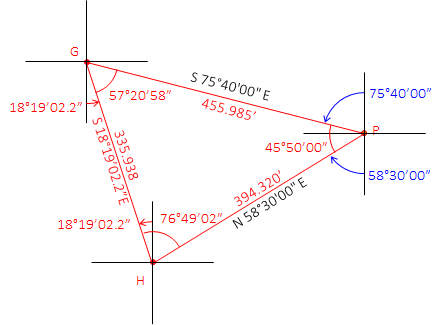Then using the Law of Sines, determine the two missing sides:

Compute point P from point G:

Math check - compute point P from point H:

check