M. Low Distortion Projections
1. Different Design Approach
The maximum distance distortions for SPC and UTM system design are 1/10,000 and 1,2500, respectively. In both cases, the distortion is from ellipsoid to grid - the grid scale k.
Measurements, however, are made at some distance removed from the ellipsoid. Reducing from ground to ellipsoid introduces another distortion. The Combined Factor, EF x k, is the total distortion from ground to grid, Figure M-1.
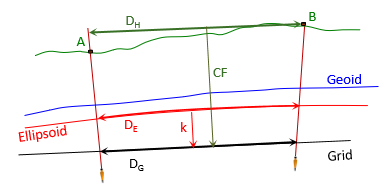 |
| Figure M-1 Distance Distortions |
Depending on location in the zone, orientation, elevation, and geoid height, the total distortion may approach or exceed the design standard. Even though distortions are systematic, their compensation adds another layer of computations and potential confusion.
2. Smaller and closer
A "perfect" grid system would be one where ground and grid distances were identical. This is impossible because of the earth's shape, but it is possible to make the differences smaller than 1/10,000. How small depends how the system is designed.
a. Smaller Area
SPC and UTM are both regional systems covering relatively larges areas and their coordinate magnitudes reflect that. Most mapping and surveying activities occur over smaller expanses.
In Chapter C, we saw that smaller distortions can be achieved by projecting a smaller area. While that may minimize ellipsoid to grid distortion, we still have to contend with elevation.
b. Near the Surface
To further minimize overall ground to grid distortion, the projection can be brought closer to the earth's surface. This is referred to as a Low Distortion Projection, LDP, Figure M-2.
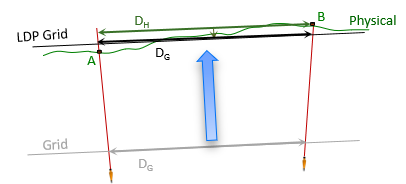 |
| Figure M-2 Low Distortion Projection |
The projection can be fit two different ways.
(1) Fit to GRS 80 Ellipsoid
Fitting to the GRS 80 ellipsoid means the projection surface may not intersect (tangent or secant) the ellipsoid, Figure M-3.
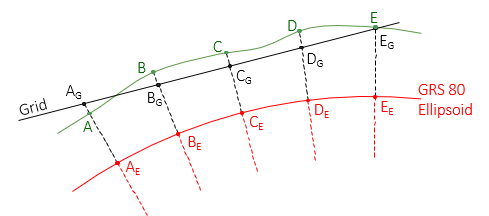 |
| Figure M-3 Projection Fit to Existing Ellipsoid |
Zone parameters are defined differently than for intersecting projections and projection equations must be modified.
(2) Fit to a New Ellipsoid
The projection can be fit conventionally (tangent or secant) to a new ellipsoid which is brought closer (raised) to the surface. This brings grid scale very close to one and balanced across the area, Figure M-4.
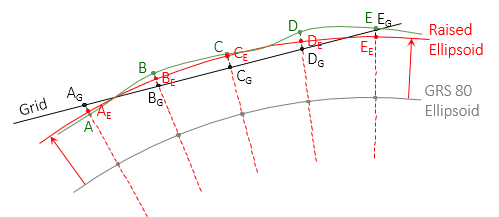 |
| Figure M-4 Projection Fit to New Ellipsoid |
Cylindric and conic projection equations are not dependent on a specific ellipsoid. Any ellipsoid can be used since its parameters (a, e, e', etc) are included in the direct and inverse conversion equations. That simplifies ellipsoid customization.
The easiest way to create a raised ellipsoid is to base it on the GRS 80 ellipsoid. A design height is determined from an area's elevation and geoid height behavior and used to bring an ellipsoid closer to the surface. The design height can be applied one of two ways.
(a) Constant height
Adding the same value, d, to both GRS 80 axes creates a parallel ellipsoid. The normal to the GRS 80 ellipsoid at a point position is also normal to the raised ellipsoid making the geodetic latitude for both surfaces the same, Figure M-5 .
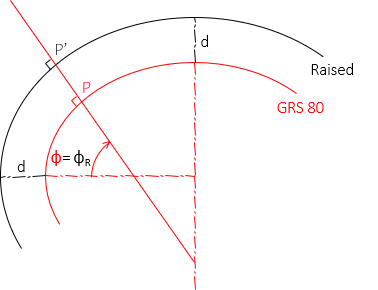 |
| Figure M-5 Constant Design Height |
| d | design height; f(elevation, geoid height) |
| Φ | GRS 80 ellipsoid latitude |
| ΦR | Raised ellipsoid latitude |
The normal is in the same meridian for both ellipsoids so the geodetic longitude is not affected. Because the geodetic coordinates do not differ, errors are not introduced between the LDP grid and GRS 80 geodetic positions.
Although parallel, the ellipsoids do not have the same geometric properties - their flattening, first and second eccentricities differ. In general this shouldn't be a problem because the projection equations include ellipsoid parameters, but some people find this disconcerting which is why differential heights can be used instead.
(b) Differential height
To keep ellipsoid relationships the same requires increasing both axes by different amounts. The design height, da=d, is added to the semi-major axis. The semi-minor axis is increased by a proportionally smaller height, db.
OK, so the ellipsoid geometry is maintained but a new problem appears: the normal to the GRS 80 ellipsoid is not normal to the raised ellipsoid, Figure M-6.
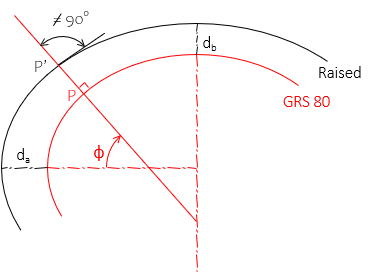 |
| Figure M-6 Differential Design Heights |
| da | design height; f(elevation, geoid height) |
| db | f(da, a, e) |
Latitude is the angle between the semi-major axis and the normal to the ellipsoid. A new normal at the raised point's position intersects the semi-major axis at a different geodetic latitude, Figure M-7.
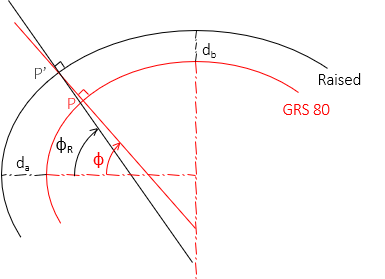 |
| Figure M-7 Different Latitudes |
The geodetic longitude is not affected since both normals are in the same meridian.
Because the two ellipsoids are rigorously connected, the latitude difference can be mathematically determined (it is a function of the latitude). This difference must be accounted for to prevent conversion errors between the LDP grid and GRS 80 geodetic positions.
c. Ground is Grid, Grid is Ground
On a carefully created LDP, grid and ground distances can be considered the same. There will be some distortion, but it will be much less than the typical distortion in an SPC or UTM system. This simplifies surveying measurements as well as mapping and GIS applications. For high accuracy needs, the remaining distortion can be compensated mathematically.
d. Software Issues
Until recently, LDP adoption, has been relatively limited; a few key implementations are discussed in the next section. Early LDP adopters encountered software problems: some converted positions incorrectly when encountering non-GRS 80 ellipsoid parameters, thinking it was a different datum. The software was not set up to recognized that LDPs referenced to raised ellipsoids had a rigorous connection between grid and geodetic coordinates and a datum change was not involved. It would apply an approximate datum-to-datum transformation instead of using the projection equations with the appropriate ellipsoid and zone parameters. This would introduce position errors, substantial in some cases. On-the-fly software would do this without the user's knowledge, other might stop and ask a confused user what to do.
This was slowly addressed by developers who incorporated existing LDPs in their software. Later LDP designs moved away from raised ellipsoids to fit ground level projections to the GRS 80 ellipsoid.
3. Existing LDPs
a. Michigan NAD 27
Michigan had two sets of SPC systems developed on NAD 27:
- A three-zone transverse Mercator cylindric system conventionally fit to the Clarke 1866 ellipsoid
- A three-zone Lambert conic system fit to a elevation 800 feet above sea level
Reason for the latter is described in C&GS Publication 65-3 Plane Projection Tables - Michigan:
To eliminate necessity for "reduction to sea level” in the great majority of surveys in the State of Michigan, advantage has been taken of the fact that Michigan is, through out most of its area, quite flat, though at an appreciable elevation above sea level. It has been determined that, except for the extreme northwestern part of the Upper Peninsula, the general Elevation of the land seldom departs much more than about 200 feet from a mean value of 800 feet above sea level. Accordingly, the coordinate system has been computed on a reference surface that is approximately 800 feet above the Clarke Spheroid of 1866 at latitude 44°.
Having two formal SPC systems could cause confusion although the cylindric system was was the more "official" of the two. For NAD 83, Michigan adopted a three-zone Lambert conic SPC system fit conventionally to the GRS 80 ellipsoid.
b. Minnesota
Minnesota was one of the first to adopt statewide LDPs. These are described in detail on Minnesota Dept of Transportation's (MNDOT) Map Projections and Parameters webpage. This section summarizes their main characteristics.
(1) NAd 27: Minnesota Project Coordinate System (MNPCS)
(a) Definition
The Minnesota Project Coordinate System of NAD 27 (MNPCS), designed by MNDOT, consisted of 50 rectangular zones, each 1 degree of
longitude by 15 minutes of latitude, Figure M-8.
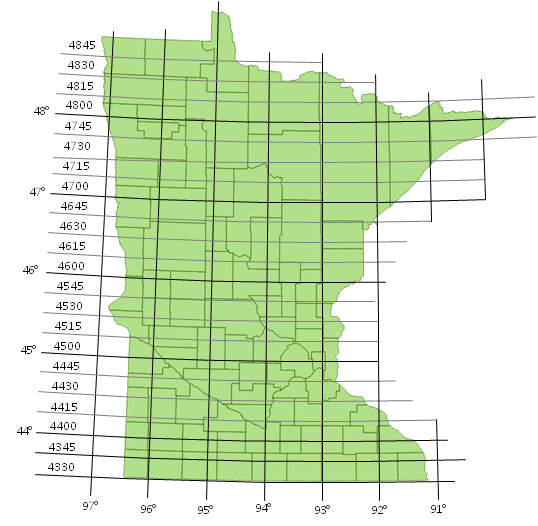 |
|
Figure M-8 |
A zone was identified by abbreviated geodetic coordinates of its southeastern corner: longitude degrees and latitude degrees and 15 minute interval. For example, the southwestern-most zone is 974330 (97°, 43°30').
(b) Mathematics
Each zone was linked directly to the SPC system. A Combined Factor, CF, was determined from a zone's mean elevation and mean SPC grid factor. Because SPC coordinates were so large, origin offsets were selected to reduce their magnitude to a more convenient size. Zone coordinates were determined by dividing SPC coordinates by the CF and adding the origin offset. The CFs and origin offsets are published on MNDOT's Minnesota Project Coordinate System of NAD 27 page.
Ground to grid distance distortion did not exceed 1/20,000. This was sufficient to consider ground and grid distances the same for most surveys at the time .
(c) Counties
MNPCS rectangular zones did not coincide with jurisdictional boundaries nor did any county fall entirely within a singe rectangular MNPCS zone - most were located in parts of two or more zones. Distortions were controlled within a zone and extending the coordinate system beyond its boundaries would introduce greater distortion. A few of the larger and more populous counties used MNPCS's design methodology to create their own single or multiple zone systems.
(2) NAD 83: Minnesota County Coordinate Projections (MNCCP)
(a) Definition
Post-NAD 83, the 1°x15" rectangular zones were abandoned in favor of a projection-based coordinate system for each county. These county systems were not linked to the SPC and were a clean re-design.
(b) Design
The MNCCP, designed by University of Minnesota faculty and graduate students, used a Lambert conic or transverse Mercator cylindric projection based on a county's configuration. A special zone along Lake Superior's western shore used an oblique Mercator cylindric projection, Figure M-9.
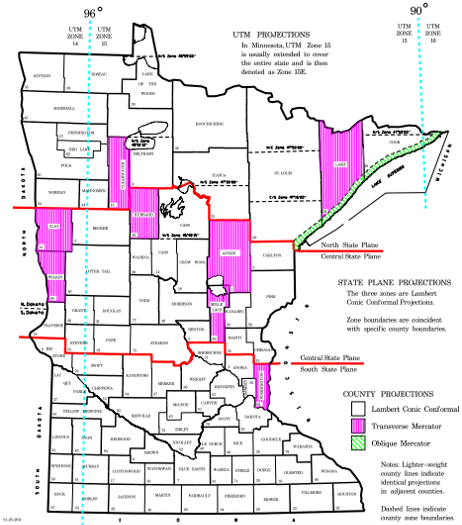 |
| Figure M-9 Minnesota County Coordinate System Source: http://www.dot.state.mn.us/surveying/pdf/mncoordsys.pdf |
There is no indication on the MNDOT website what was used for a maximum design distortion.
(c) Mathematics
An average ellipsoid height was determined for each county based on its mean elevation and geoid height.
- Lambert conic counties
A raised ellipsoid was created by increasing the GRS 80 ellipsoid semi-major axis by the height and the semi-minor axis by a proportional amount to maintain geometry as described in Section B.2.b(2).
Coordinate conversion and grid distance reduction distances are done with the conic projection equations in NOAA Manual NOS NGS 5 State Plane Coordinate Systems of 1983 using individual county parameters and semi-major axes listed on the NAD 83 Minnesota County Coordinate System page of the MNDOT website.
No mention is made about the latitude correction discussed in Section B.2.b(2). Hmm...
- Transverse Mercator cylindric counties
The height is not added to the GRS 80 semi-major axes prior to coordinate conversion. Instead, an Elevation Factor, EF, is defined for a county using the earth radius and its average ellipsoid height.
The EF is used to convert between county coordinates and those from the NOAA Manual NOS NGS 5 cylindric projection equations using county parameters. The parameters are listed on the NAD 83 MNCCS page.
c. Illinois NAD 83
The Illinois State Plane Coordinate System Committee (ISPCSC) recently (2021) developed the Illinois Coordinate System of 1983: 33 Zone Layer (ICS83: 33 Zone). As its name implies, it consists of 33 LDP grids covering the state of Illinois, Figure M-10.
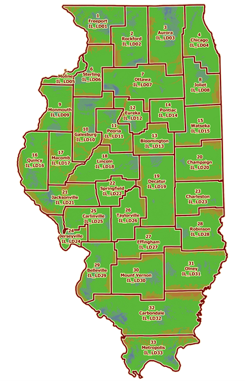 |
| Figure M-10 ICS83: 33 Zone Source: IL Geospatial Data Clearninghouse |
Zones were designed following NGS NATRF2022 LDP standards described in Section 6 of Procedures for Design and Modification of the State Plane Coordinate System of 2022 which, despite its name, also applies to LDPs. Near-ground grids are based on non-intersecting projections fit to the GRS 80 ellipsoid, similar to the condition shown in Figure M-4.
There are:
- Nineteen zones on conic projections: These use a single standard parallel conic projection whose equations differ from a two standard parallel conic used for SPC and other LDP systems.
- Fourteen zones on transverse cylindric projections
Reported grid-ground distortions are less than 20 ppm (= 1/50,000) over 99% of the state.
Basic information, parameters, and software are at the ICS83: 33 Zone page on the IL Geospatial Data Clearinghouse website.
d. Oregon NAD 83
Oregon begacn development of its Oregon Coordinate Reference Systems in the mid 2000's. A list of 20 best practices goals were estbliahed to guide development of the zones. Among the more critical were
- 1/100,000 maximum ground-grid distortion
- Use conventional conic, transverse cylindric, and oblique cylindric projections
- No ellipsoid modification
- Referenced to the NSRS
- Zone extents would not be jurisdictionally limited
- Publication of a Handbook and User Guide
- Involve vendors and developers so zone parameters would be included in commercial software.
Because of Oregon's varying terrain, 39 overlapping zones were developed, Figure M-11.
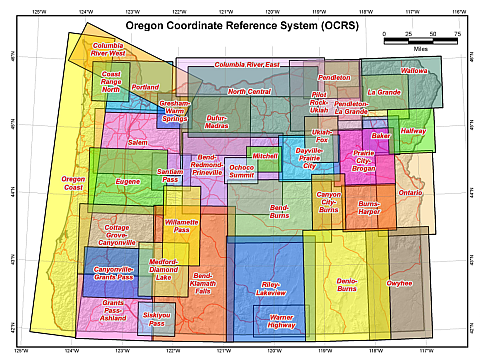 |
| Figure M-11 Oregon Coordinate Reference Systems |
More information is on the Oregon Coordinate Reference System website.
BTW - Oregon uses the International Foot definition to relate Imperial and Metric linear systems.
e. Wisconsin NAD 83
(1) Wis County Coordinate System (WCCS)
Wisconsin was another early adopter of statewide LDPs although it was after the NAD 83 (91) adjustment. In the early 1990s the Wis Dept of Transportation (WIDOT) contracted for the development of an LDP for each of the state's 72 counties. The project was completed in 1993 and named the Wisconsin County Coordinate System (WCCS).
Maximum allowable ground-to-grid distortions of 1/30,000 in rural areas and 1/50,000 in urban areas were specified. An ellipsoid height was determined for each county based on its median elevation and average geoid height. The ellipsoid height was added to both axes of the GRS 80 ellipsoid to create a parallel raised ellipsoid for the county. Depending on county configuration, a conic or cylindric projection was used to create the grid system.
Due to their size and/or elevation variation, some counties were combined into a single coordinate system and still met the distortion specifications. Figure M-12 is a map of Wisconsin counties. Counties shown in white have their own coordinate systems; counties that share a coordinate system are shown in the same color.
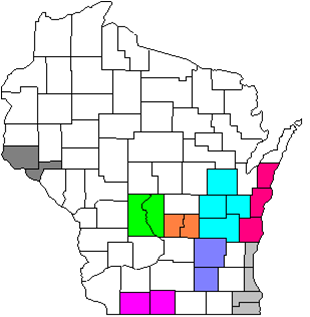 |
| Figure M-12 Wis County Coordinate Systems |
WCCS consisted of 59 systems covering 71 counties. Jackson County in west-central Wisconsin is not part of WCCS: the County Surveyor created a system prior to WCCS implementation.
County coordinates were computed directly from the NOAA Manual NOS NGS 5 projection equations using the county's parameters and raised ellipsoid data - no other computations or modifications are needed. Parameters and a distortion analysis for each county is available on the Wisconsin State Cartographer's Office (SCO) website.
WCCS system was immediately adopted by most counties and major municipalities on which to build their geographic information systems (GIS).
(2) Wisconsin Coordinate Reference System (WisCRS)
Although WCCS was popular and widely used, some GIS users reported position errors when combining data from different coordinate systems. This was the software issue described in Section B.4: some software treated coordinate conversion as a datum-to-datum transformation instead of a rigorous conversion because of the raised ellipsoid parameters. The Wisconsin Land Information Association created a Task Force to examine the issue and identify ways it could be resolved.
After a series of meetings and with input from diverse groups of stakeholders, the Task Force decided the county LDPs should be redesigned and referenced directly to the GRS 80 ellipsoid. Moreover, because so many users had data based on WCCS, the new systems had to be accuracy compatible: maximum position difference could not fall outside ±5 mm. This required new parameters and using a single-parallel projection for conic systems.
The redesigned coordinate systems were completed in 2009. WisCRS is actually the collection of all the formal coordinate systems in Wisconsin, of which the county LDPs are a subset.
Parameters and a distortion analysis for each county is in the second edition of the Wisconsin Coordinate Reference Systems handbook on the SCO website.
More information including equations for a single-parallel conic projection, county-by-county WCCS-WisCRS position comparisons, and software utilities are on the SCO's Coordinate Reference Systems webpage.
Although WisCRS county systems were intended to replace WCCS, both sets of county systems generally appear in many software packages.
4. Future LDP Development
The current horizontal and vertical datums will be replaced by a single 3D datum, the North American Terrestrial Reference Frame of 2022 (NATRF2022); planned completion is 2024. In conjunction with the new datum, the NGS will redesign state coordinate systems. Each state will have:
- a single statewide coordinate system (mapping quality)
- an updated SPC (SPCS2022) system consisting of one or more zones (survey quality)
SPCS2022 will use tighter distortion standards than the current 1/10,000.
NGS also will design and support a "limited" number LDPs for a state. Original NGS policy was to avoid developing and maintaining an extremely large number of coordinate systems. States with existing LDPs have petitioned NGS for an exemption to incorporate their systems.
Most states have formed committees or task forces who interface with NGS on system design and implementation issues.
This is a very brief summary of the NATRF2022 and future coordinate systems. Detailed information, publications, and webinars are accessible on the New Datums page of the NGS website.