2. 3D to 2D

a. You sat toe-may-toe, I say toe-mah-toe...

Although we've defined an ideal reference system, we still have a problem: projecting the 3D Earth into a 2D plane.

The tomato in Figure C-4 represents the Earth and the 2D plane the coordinate system.

Figure C-4 Earth and Plane

What happens when we project the tomato into the plane, Figure C-5? 

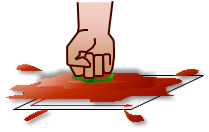Figure C-5 Project!

The tomato must be distorted to fit into the plane. A 3D object cannot be projected into a 2D plane without introducing some distortions.
(Why a tomato? I was forced to eat them as a kid so I take advantage of every chance to exact vengeance on them.)

b. Orange Peel Map

Figure C-6 is an orange on which a globe has been copied. To project it into a 2D plane, the orange is carefully peeled, attempting to keep the peel in one piece although it will tear in a number of places.

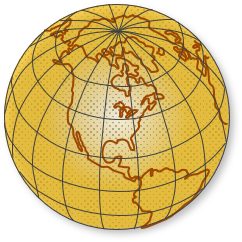Figure C-6 3D Globe

It's laid it out flat creating an orange peel map, Figure C-7.

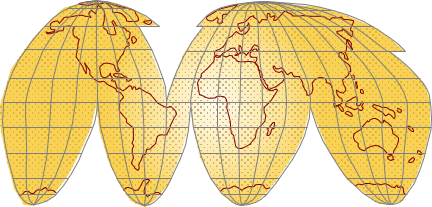Figure C-7 Orange Peel Map

Some areas will lay flat without change. Others will stretch or shrink a little without tearing if the peel has some elasticity.

Adding North and East axes creates a grid coordinate system. Figure C-8 shows this and indicates a few of the many problems.

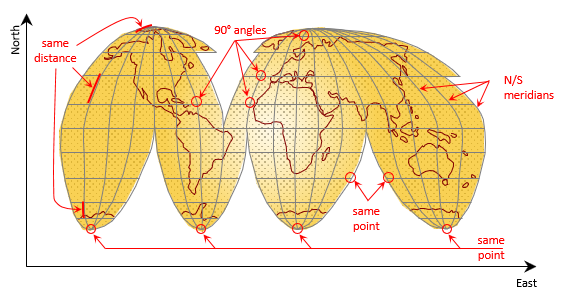Figure C-8 Distortions

The angle between the equator at each meridian is very close or equal to 90°. North and south of the equator, angles between meridians and east-west lines differ from 90° by varying amounts.

Meridians uniformly converge to the two poles on the globe. When projected, along the equator they are equally spaced and roughly parallel. Going north and south, they are are bent into various shapes and do not converge on just two points.

A single point on the globe can have multiple physical representations on the coordinate system:

• The south pole is repeated four times, the north twice.
• Points along tear lines have two sets of coordinates

Shape and size are affected, the amount depending on location in the projected area. Note how much Anarctica's shape is affected versus Africa's .