4. Interpolation Pairs

Which point pairs should be used for interpolation? There are six possible interpolation paths, Figure E-10, for the four point data set of Figure E-1.

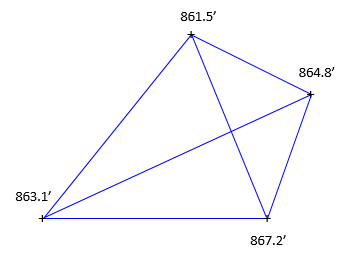Figure E-10 Interpolation Paths

As more data points are added, the number of interpolation paths grows geometrically. How many are enough?

Another issue is the ground slope between points. Can it be assumed uniform along every path? Consider the modestly sized data set in Figure E-12.

Figure E-12 Area Data Set

The 858.7 data point (highlighted) will anchor one end of multiple interpolation paths, many of which are shown in Figure E-13.

Figure E-13 Interpolations from 858.7

While uniform slopes to nearby points are reasonable, that's not the case for points further away. Data collection in the field takes into account terrain in the data point's vicinity. Consider the northernmost 896.8 point: it was not selected based on the 858.7 data point. It's also highly unlikely the ground is uniform between points that far apart.

Using a point's nearest neighbors makes the most sense, Unfortunately, what constitutes "nearest" differs based on data density variation across the entire data set. It's also hard to program in software.

Fortunately, there is a systematic way to determine which data pairs to use: Triangulated Irregular Networks (TIN).