2. Interpolation

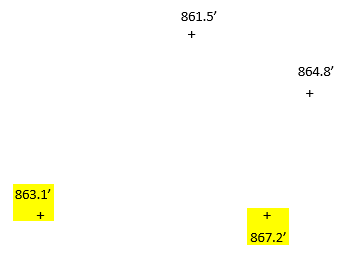
The ground slope between any two data points is assumed uniform which allows interpolation between them to locate contours. Figure E-1 is a subset of four three-dimensional (3D) data points.

Figure E-1 Data Points

Each point is plotted at its horizontal location, indicated by the + symbol, and labeled with its elevation. The data will be used to create a two foot contour interval representation.

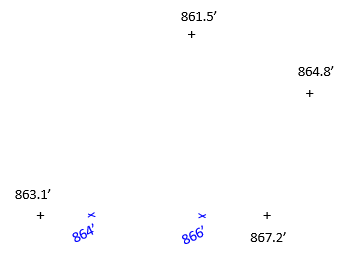
Starting with the two highlighted southern points, the 864 ft and 866 ft contour lines pass somewhere between them. Since a uniform slope is assumed,  864 ft and 866 ft would cross at proportional distances between the data points.

To interpolate:

The elevation difference is 867.2-863.1 = +4.1 ft
Measure the distance between the points, call it D.

From the 863.1 ft point to 864 ft:

Elev diff = 864-863.1 = +0.9 ft
(dist/D) = (+0.9/+4.1);   dist = (0.9/4.1)D

From the 863.1 ft point to 866 ft:

Elev diff = 866-863.1 = +2.9 ft
dist = (2.9/4.1)D

The interpolated points are shown in Figure E-2.

Figure E-2 864 ft and 866 ft Crossings

Additional interpolations would be done between different combinations of coordinate pairs. Figure E-3 shows the results from interpolating around the perimeter.

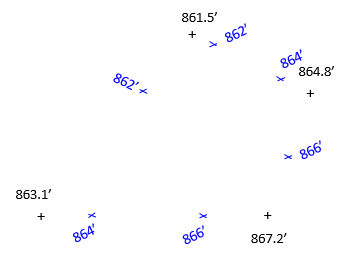Figure E-3 Perimeter Crossings

Contour lines are drawn by connecting the respective interpolated points.

There are two issues with this method

• Lots of computations
• Interpolation pairs

Let's address these in turn.