Page 7 of 8
c. Crossing Loop Traverse
As long as a traverse closes back on its beginning point, it can be adjusted the same as any other loop traverse.
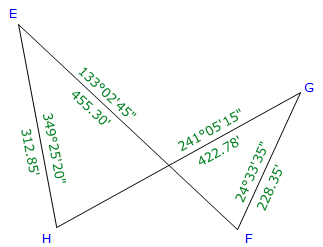 |
| Figure E-8 Crossing Loop Traverse Example |
| Line | Azimuth | Length (ft) | Lat (ft) | Dep (ft) |
| EF | 133°02'45" | 455.30 | -310.780 | +332.737 |
| FG | 24°33'35" | 228.35 | +207.691 | +94.912 |
| GH | 241°05'15" | 422.78 | -204.403 | -370.084 |
| HE | 349°25'20" | 312.85 | +307.534 | -57.430 |
| sums: | 1419.28 | +0.042 | +0.135 | |
| Dist | Lat err too far N |
Dep err too far E |
(1) Adjust and recompute each line.
Setup Equations E-1 and E-2:
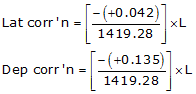
Solve Equations E-3 and E-4 for each line:
Line EF
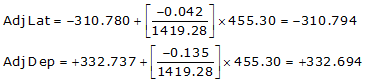
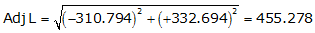
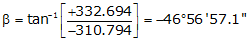
Because it's in the SE quadrant: Az = 180°00'00"+(-46°56'57.1") = 133°03'02.9"
Line FG
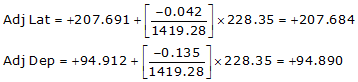
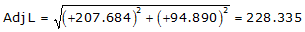
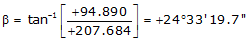
Because it's in the NE quadrant: Az = 24°33'19.7"
Line GH
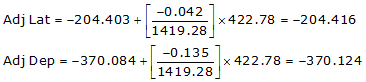
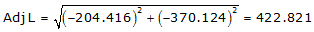
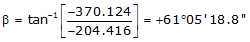
Because it's in the SW quadrant: Az = 180°00'00"+(61°05'18.8") =241°05'18.8"
Line HE
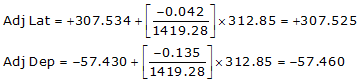
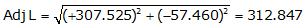
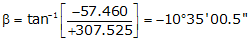
Because it's in the NW quadrant: Az = 360°00'00"+(-10°35'00.5") = 349°24'59.5"
(2) Adjustment summary
| Adjusted | Adjusted | |||
| Line | Lat (ft) | Dep (ft) | Length (ft) | Azimuth |
| EF | -310.794 | +332.694 | 455.278 | 133°03'02.9" |
| FG | +207.684 | +94.890 | 228.335 | 24°33'19.7" |
| GH | -204.416 | -370.124 | 422.821 | 241°05'18.8" |
| HE | +307.525 | -57.460 | 312.847 | 349°24'59.5' |
| sums: | -0.001 | 0.000 | ||
| check (rounding) | check | |||