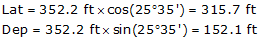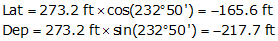D. Latitudes and Departures
1. Definition; Equations
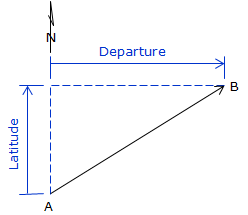
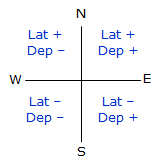
Latitude is the north-south component of a line; departure the east-west. North latitudes are positive, South are negative; similarly East departures are positive, West are negative.
|
|
|
|
(a) |
(b) |
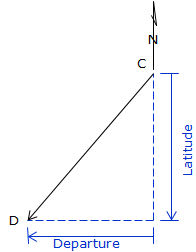
| Figure D-1 Latitudes and Departures |
|
Latitude (Lat) and Departure (Dep) are computed from:
| Equations D-1 and D-2 |
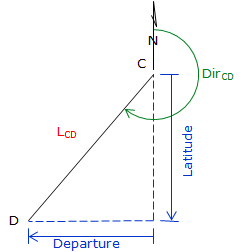
Dir can be either a bearing angle, Figure D-2(a), or azimuth angle, Figure D-2(b).
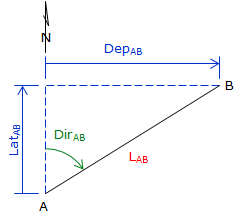 |
 |
|
(a) |
(b) |
| Figure D-2 Bearings or Azimuths |
|
Because a bearing angle never exceeds 90°, the Lat and Dep equations will always return positive values.
|
|
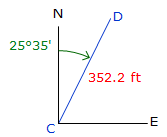
Sin(0°) to Sin(90°) ranges from 0 to +1.0 Cos(0°) to Cos(90°) ranges from +1.0 to 0 The correct mathematical sign for the Lat and Dep come from the bearing quadrant. A bearing of S 47°35' E has a negative Lat (South) and a positive Dep (East). |
| Figure D-3 Quadrants |
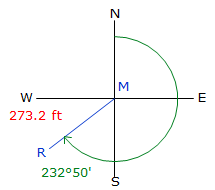
An azimuth angle ranges from 0° to 360°, so the sine and cosine return the correct signs on the Lat and Dep.
Examples
|
|
|
| Figure D-4 NE Azimuth |
|
|
|
|
| Figure D-5 SW Azimuth |
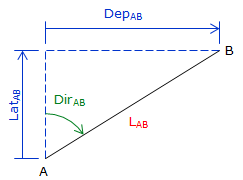
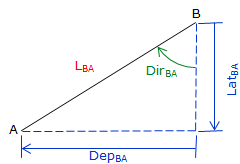
Reversing a line direction results in the same magnitude Lat and Dep but reversed signs:
| Line A to B | Line B to A |
 |
 |
| (a) | (b) |
| Figure D-6 Reverse Latitude and Departure |
|