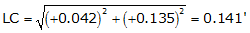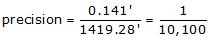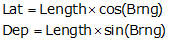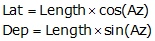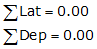3. Examples
In the following examples shown, all calculations are shown with an additional significant figure. Because these are generally intermediate computations, carrying an additional digit minimizes round-off error in subsequent calculations.
When reporting results of an intermediate calculation, those should be stated to the correct number of significant figures so as not to imply an accuracy beyond that of the measurements.
a. Traverse with bearings
|
|
Lat and Dep will always compute as positive; must assign correct mathematical sign based on the bearing quadrant.
|
||
| Figure D-10 Bearing Traverse |
Line AB
![]()
Because the bearing is South and West, the Lat and Dep are -176.357' and -438.548' respectively.
Line BC
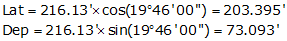
Because the bearing is North and West, the Lat and Dep are +203.395' and -73.093' respectively.
Line CD
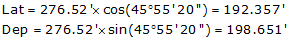
Because the bearing is North and East, the Lat and Dep are +192.357' and +198.651' respectively.
Line DA
![]()
Because the bearing is South and East , the Lat and Dep are -219.312' and +313.065' respectively
In tabular form:
|
Line |
Bearing |
Length (ft) |
Lat (ft) |
Dep (ft) |
|
AB |
S 68°05'35"W |
472.68 |
-176.357 |
-438.548 |
|
BC |
N 19°46'00"W |
216.13 |
+203.395 |
-73.093 |
|
CD |
N 45°55'20"E |
276.52 |
+192.357 |
+198.651 |
|
DA |
S 54°59'15"E |
382.24 |
-219.312 |
+313.065 |
|
sums: |
1347.57 |
+0.083 |
+0.075 |
|
|
Distance |
Lat err |
Dep err |
||
|
|
too far N |
too far E |
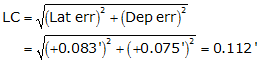
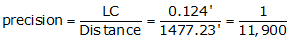
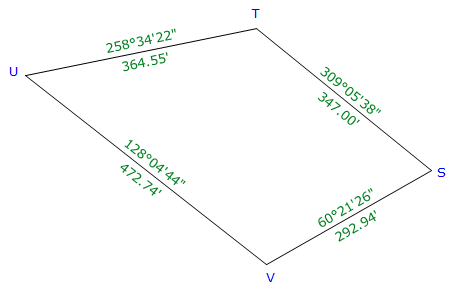
b. Traverse with azimuths
|
|
Lat and Dep will always compute directly with the correct sign when using azimuths. |
||
| Figure D-11 Azimuth Traverse |
Line ST
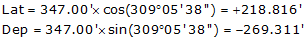
Line TU
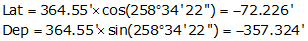
Line UV
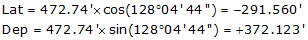
Line VS
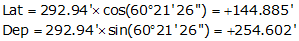
|
Line |
Azimuth |
Length (ft) |
Lat (ft) |
Dep (ft) |
|
ST |
309°05'38" |
347.00 |
+218.816 |
-269.311 |
|
TU |
258°34'22" |
364.55 |
-72.226 |
-357.324 |
|
UV |
128°04'44" |
472.74 |
-291.560 |
+372.123 |
|
VS |
60°21'26" |
292.94 |
+144.885 |
+254.602 |
|
sums: |
1477.23 |
-0.085 |
+0.090 |
|
|
Distance |
Lat err |
Dep err |
||
|
too far S |
too far E |
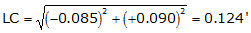
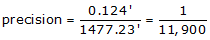
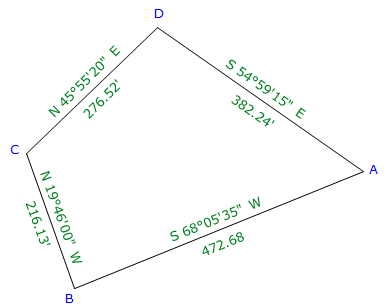
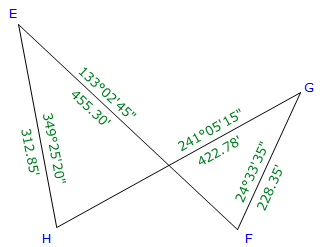
c. Crossing Traverse
A four-sided parcel has two obstructed lines.
 |
| Figure D-12 Parcel Boundaries |
In order to create a closed traverse, the survey crew measures a crossing traverse which connects all four points.
|
|
As long as a traverse closes back on its beginning point, the closer condition is still:
regardless of how many times it may cross itself.
Given this traverse data, determine its closure and precision.
|
|
Figure D-13 |
Rather than write out each Lat and Dep computation separately, we can simply set up the table and record the computations in it.
|
Line |
Azimuth |
Length (ft) |
Lat (ft) |
Dep (ft) |
|
EF |
133°02'45" |
455.03 |
-310.780 |
+332.737 |
|
FG |
24°33'35" |
228.35 |
+207.691 |
+94.912 |
|
GH |
241°05'15" |
422.78 |
-204.403 |
-370.084 |
|
HE |
349°25'20" |
213.85 |
+307.534 |
-57.430 |
|
sums: |
1419.28 |
+0.042 |
+0.135 |
|
|
Distance |
Lat err |
Dep err |
||
|
too far N |
Too far E |