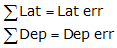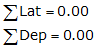E. Traverse Adjustment
1. Adjusting a Traverse
Adjusting a traverse (also known as balancing a traverse) is used to distributed the closure error back into the angle and distance measurements.
|
Summing the latitudes and departures for the raw field traverse:
|
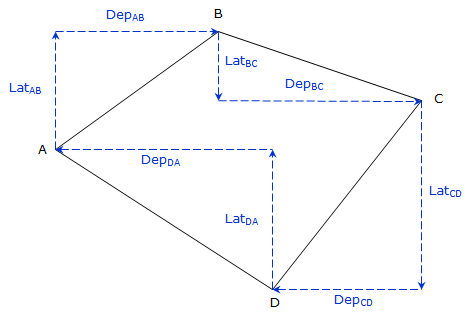 |
||
| Figure E-1 Loop Traverse Misclosure |
|||
|
On an adjusted (balanced) traverse:
|
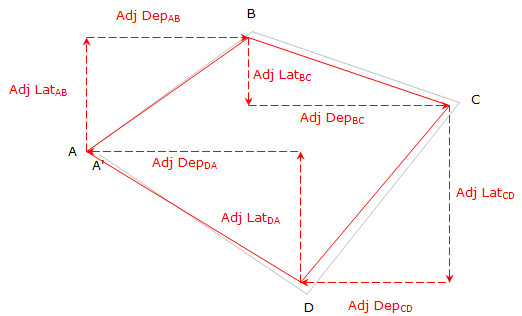 |
||
| Figure E-2 Adjusted (Balanced) Loop Traverse |
The condition for an adjusted traverse is that the adjusted Lats and Deps sum to 0.00. As with other survey adjustments, the method used to balance a traverse should reflect the expected error behavior and be repeatable. Table E-1 lists primary adjustment methods with their respective advantages and disadvantages.
| Table E-1 | |||
| Method | Premise | Advantage | Disadvantage |
| Ignore | Don't adjust anything. | Simple; repeatable | Ignores error |
| Arbitrary | Place error in one or more measurements | Simple | Not repeatable; ignores error behavior |
| Compass Rule | Assumes angles and distances are measured with equal accuracy so error is applied to each. | Simple; repeatable; compatible with contemporary measurement methods. | Treats random errors systematically |
| Transit Rule | Assumes angles are measured more accurately than distances; distances receive greater adjustment. | Simple; repeatable; compatible with older transit-tape surveys. | Treats random errors systematically; not compatible with contemporary measurement methods. |
| Crandall Method | Quasi-statistical approach. Angles are held and errors are statistically distributed into the distances. | Allows some random error modeling; repeatable. | Models only distance errors, not angle errors. |
| Least squares | Full statistical approach. | Allows full random error modeling; repeatable; can mix different accuracy and precision measurements; provides measurement uncertainties. | Most complicated method |
Most simple surveying projects use total stations which measure distances and angles with comparable quality. The Compass Rule is an appropriate adjustment method for these traverses. Although least squares would provide a "better" adjustment solution, it is generally overkill for a basic traverse. For more information on traverse adjustment by least squares see XVIII. Least Squares Lite.
We will concnetrate on the Compass Rule.