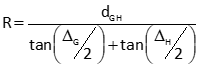C. Three-tangent arc

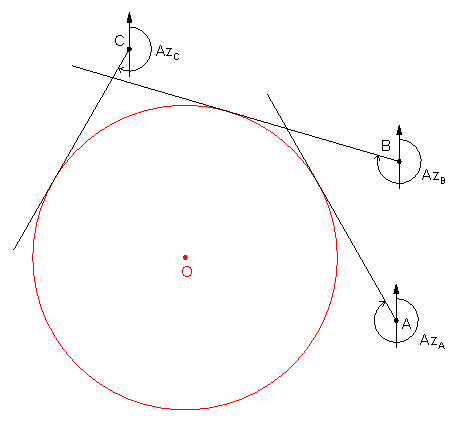
Three non-colinear intersecting lines can serve as tangent lines to define a circle, Figure I-5.

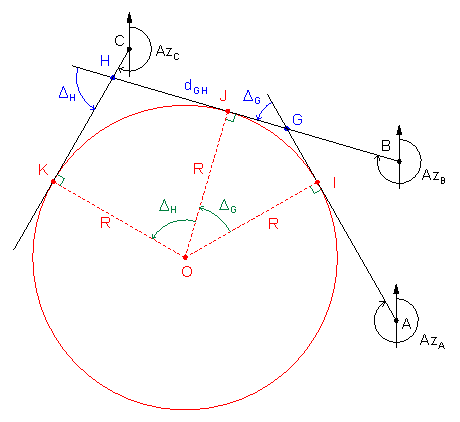
Figure I-6 shows the primary geometry of the three-tangent arc.  

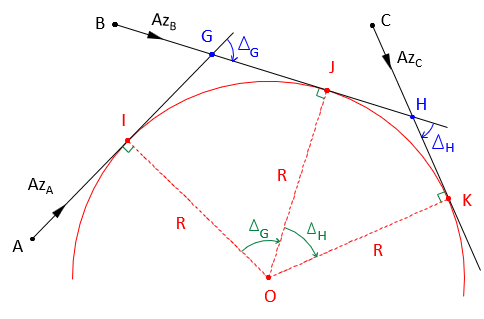
Figure I-7 shows geometry for a curver to the right, as defined by the tangent azimuths.

Points I, J, and K are the tangent points. These divide the curve into two tangent arcs having the same radius with points G and H as their Points of Intersection (PI).

Solution process

Determine PIs, G and H, by direction-direction intersection. Inverse between them to obtain the distance, d_GH.

Using the azimuths, compute deflection angles Δ_G and Δ_H at the PIs.

Compute curve radius using Equation I-19

R is positive for a curve to the right; negative for a curve to the left.

Distances d_GJ and d_GI are the tangent distances for the first curve; distances d_HK and d_HJ are the tangent distances for the second curve. To compute an arc's tangent distance use:

Equation I-20

To compute the coordinates of the radius point

• Forward Computation from point G to point J using Az_B and tangent distance d_GJ
• Compute azimuth to the radius point,  Az_JO, by adding (curve to right) or subtracting (curve to left) 90° to/from Az_B.
• Forward Computation from point J to point O using Az_JO and R.

The coordinates of the radius point can also be computed by Forward Computation sequences:

• Point G to point I to point O
• Point H to point J to point O
• Point H to point K to point O