B. Tangent line-arc intersection

The next two solutions deal with tangent a tangent line and arc.

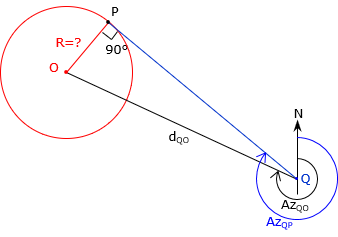
1. Radius from line direction and radius point

Known information

• Coordinates at point Q
• Direction from point Q
• Coordinates of radius point, point O

Determine

• Radius of tangent arc
• Coordinates of tangent point P

Solution process

Inverse along the line from point Q to the radius point, O, to determine the direction and length of the line.

Compute angle Q as the difference between the directions Az_QO and Az_QP, subtracting the smaller from the larger, depending on which side of line QO line QP is.

Solve the following equations

	Equation I-8
	Equation I-9
	Equation I-10
	Equation I-11

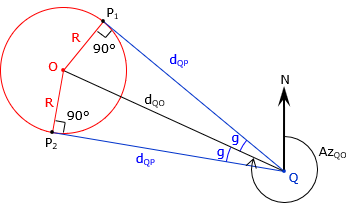
2. Line direction from radius point and radius

Known information

• Coordinates of radius point, point O
• Arc radius
• Coordinates of point Q

Determine

• Direction of a line from point Q tangent to the arc; there are two possible directions, compute both
• Coordinates of the two tangent points P₁ and P₂

Determine the direction of a line tangent to an arc.

Solution process

Inverse along the line from point point Q to the radius point O to determine its direction and length.

Compute angle g using Equation I-12.

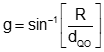Equation I-12

Angle g is used with the direction of line point Q to radius point O to determine the direction from point Q to each intersection point.

The distance from point Q to each intersection point is:

Equation I-13

To compute the coordinates of P₁, perform a Forward Computation from point Q:

	Equation I-13
	Equation I-14
	Equation I-15

To compute the coordinates of point P₂, perform a Forward Computation from  point Q:

	Equation I-16
	Equation I-17
	Equation I-18