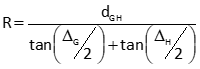I. Curve and Line-Curve Fits
This chapter explains several curve and tangent line-curve fitting situations. They can be used with other COGO tools to construct complex curvilinear traverses having to fit specific mathematical conditions.
A. Fitting arc through three points
Three non-linear points define a circular arc, Figure I-1
 |
| Figure I-1 Three point arc |
If the coordinates of the three points (1, 2, and 3) are known, the arc radius (R) and radius point (O) coordinates can be determined.
Equations I-1 and I-2 are used to compute the radius point coordinates.
| Equation I-1 | |
| Equation I-2 |
The coefficients for Equation I-1 are:
| Equation I-3 | |
| Equation I-4 | |
| Equation I-5 | |
| Equation I-6 |
Once the radius point coordinates are determined, the arc radius can be computed from Equation I-7 .
| Equation I-7 |
Point i is any of the three points used to define the arc.
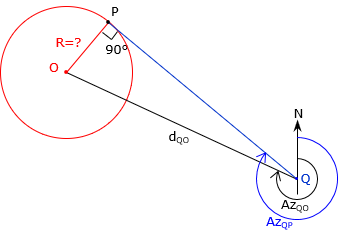
B. Tangent line-arc intersection
The next two solutions deal with tangent a tangent line and arc.
1. Radius from line direction and radius point
Known information
- Coordinates at point Q
- Direction from point Q
- Coordinates of radius point, point O
Determine
- Radius of tangent arc
- Coordinates of tangent point P
|
|
|
Figure I-2 |
Solution process
Inverse along the line from point Q to the radius point, O, to determine the direction and length of the line.
Compute angle Q as the difference between the directions AzQO and AzQP, subtracting the smaller from the larger, depending on which side of line QO line QP is.
Solve the following equations
| Equation I-8 | |
| Equation I-9 | |
| Equation I-10 | |
| Equation I-11 |
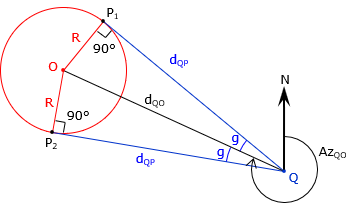
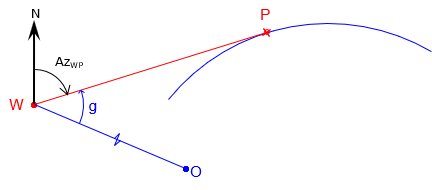
2. Line direction from radius point and radius
Known information
- Coordinates of radius point, point O
- Arc radius
- Coordinates of point Q
Determine
- Direction of a line from point Q tangent to the arc; there are two possible directions, compute both
- Coordinates of the two tangent points P1 and P2
Determine the direction of a line tangent to an arc.
|
|
|
Figure I-3 |
Solution process
Inverse along the line from point point Q to the radius point O to determine its direction and length.
Compute angle g using Equation I-12.
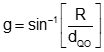 |
Equation I-12 |
Angle g is used with the direction of line point Q to radius point O to determine the direction from point Q to each intersection point.
The distance from point Q to each intersection point is:
| Equation I-13 |
To compute the coordinates of P1, perform a Forward Computation from point Q:
| Equation I-13 | |
| Equation I-14 | |
| Equation I-15 |
To compute the coordinates of point P2, perform a Forward Computation from point Q:
| Equation I-16 | |
| Equation I-17 | |
| Equation I-18 |
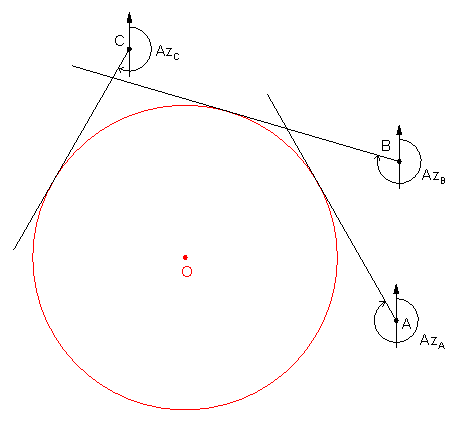
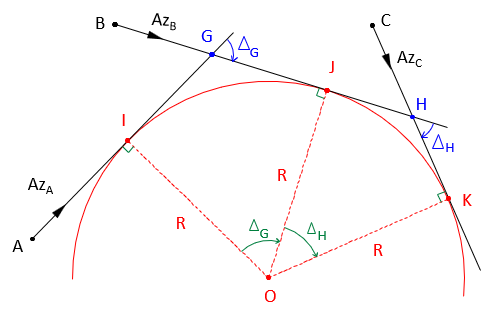
C. Three-tangent arc
Three non-colinear intersecting lines can serve as tangent lines to define a circle, Figure I-5.
|
|
|
Figure I-5 |
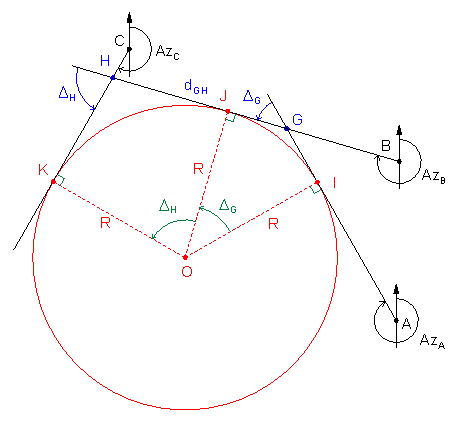
Figure I-6 shows the primary geometry of the three-tangent arc.
|
|
|
Figure I-6 |
Figure I-7 shows geometry for a curver to the right, as defined by the tangent azimuths.
|
|
|
Figure I-7 |
Points I, J, and K are the tangent points. These divide the curve into two tangent arcs having the same radius with points G and H as their Points of Intersection (PI).
Solution process
Determine PIs, G and H, by direction-direction intersection. Inverse between them to obtain the distance, dGH.
Using the azimuths, compute deflection angles ΔG and ΔH at the PIs.
Compute curve radius using Equation I-19
|
|
Equation I-19 |
R is positive for a curve to the right; negative for a curve to the left.
Distances dGJ and dGI are the tangent distances for the first curve; distances dHK and dHJ are the tangent distances for the second curve. To compute an arc's tangent distance use:
| Equation I-20 |
To compute the coordinates of the radius point
- Forward Computation from point G to point J using AzB and tangent distance dGJ
- Compute azimuth to the radius point, AzJO, by adding (curve to right) or subtracting (curve to left) 90° to/from AzB.
- Forward Computation from point J to point O using AzJO and R.
The coordinates of the radius point can also be computed by Forward Computation sequences:
- Point G to point I to point O
- Point H to point J to point O
- Point H to point K to point O
D. Examples
1. Three point curve
Three known coordinate points are
| Point | North (ft) | East (ft) |
| A | 902.72 | 1751.91 |
| B | 870.76 | 1237.76 |
| C | 538.57 | 1293.16 |
Determine the radius of the circle passing through the points and coordinates of the radius point.
Sketch
Compute the coefficients using Equations I-3 through I-6
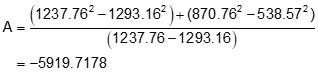
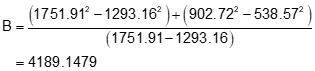

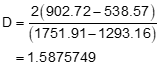
Use the coefficients in Equations I-1 and I-2 to get radius point coordinates
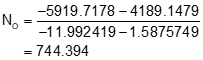
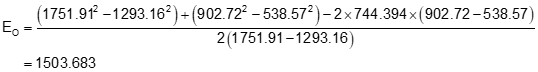
Get radius from Equation I-7
Using point A
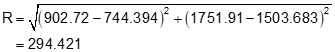
Check using point B
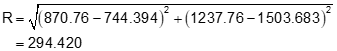
Checks within rounding.
Answers
| Radius | 294.42' | |
| Radius pt coords | 744.39' N | |
| 1503.68' E |
2. Tangent line
What is the direction of the line line tangent to the arc shown below? What are the coordinates of the intersection point?
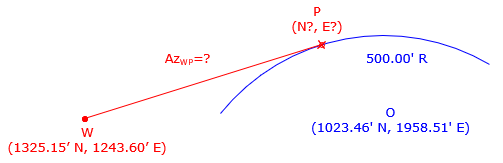
Inverse from point W to the radius point O
![]()
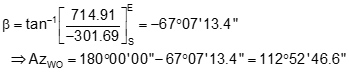
![]()
Using Equation I-12 compute the angle g between the line to the radius point and tangent line.
![]()
Determine the azimuth and length of the tangent line
.
Since the tangent line is left of the line to the radius point, to get its azimuth subtract g from AzWO' Equation, I-16.
![]()
Its length comes from Equation I-13
![]()
Forward Computation, Equations I-17 and I-18, to compute tangent point coordinates
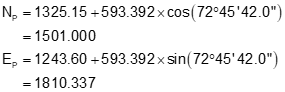
Answers
| Tangent azimuth | 72°45'42" | |
| Tangent pt coords | 1501.00' N | |
| 1810.34' E |
3. Three-tangent arc
What is the radius of the arc that is tangent to the three line shown?
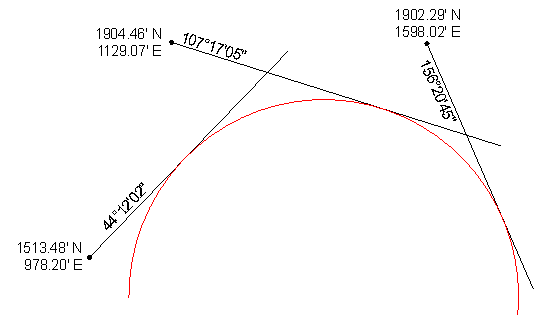
Label the geometry
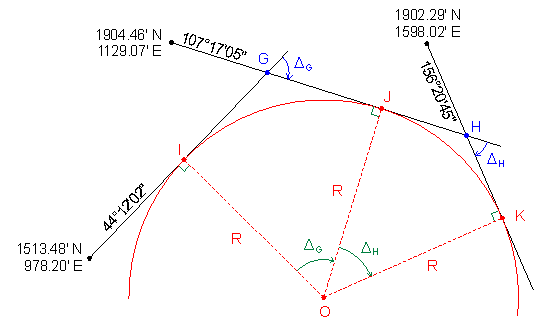
Establsh points G and H using direction-direction intersections (results shown, comps left to user)
| Point | North | East |
| G | 1849.672 | 1305.139 |
| H | 1735.850 | 1670.923 |
ΔG and ΔH from the azimuths (comps left to user)
| ΔG | 63°05'03" |
| ΔH | 49°03'40" |
Inverse Computation to obtain distance from point G to point H (comps left to user): 383.084
Apply Equation I-19 to get the arc radius
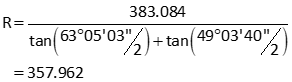
Tangent distance for first arc section (comps left to user): 219.721
Radius point coordinates (comps left to user): 1,442.592' N and 1,408.580' E
Answers
| Radius | 357.96' | |
| Radius pt coords | 1,442.59' N | |
| 1,408.58' E |