H. Area
1. Traverse with straight sides
a. Closed polygon
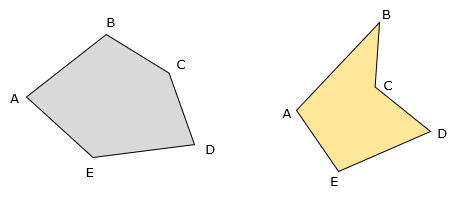
The area of any closed non-crossing polygon, Figure H-1,
|
|
|
Figure H-1 |
can be computed using the coordinates of its verticies with Equation H-1:
|
|
Equation H-1 |
This equation works for any polygon with straight sides. The more verticies, the more terms in the equation. An easy way to remember equations is graphically:
|
Starting at one point, list the coordinates in sequence around the exterior. Repeat the first point at the end. |
|
|
Cross-multiply the coordinates. |
|
|
Sum the cross-products.
|
|
| Subtract one sum from the other, divide the result by two, and take the absolute value. This is the polygon area. |
|
It doesn't matter:
- at which point you start
- going clockwise or counterclockwise around the polygon
- whether coordinates are East-North or North-East
The last two can affect the area's mathematical sign which is why Equation H-2 uses the absolute value.
b. Example area computation
Determine the area of the traverse in Figure H-2.
|
|
|
Figure H-2 |
Set up the coordinates table with additional rows for first point repetition and sums and two columns for cross-products.
We'll start at point C, travel clockwise, and carry an extra significant figure to minimize cumulative rounding.
| Point | North (ft) | East (ft) | ||
| C | 406.31 | 1259.97 | ||
| D | 235.12 | 1489.47 | ||
| E | 65.81 | 1126.40 | ||
| A | 317.89 | 942.04 | ||
| B | 675.32 | 1282.54 | ||
| C | 406.31 | 1259.97 | ||
| sums: |
Partial cross-products:
![]()
406.31 x 1489.47 = 605,187
235.12 x 1126.40 = 264,489
...
![]()
235.12 x 1259.97 = 296,244
65.81 x 1489.47 = 98,022
...
The units on the cross-products are square feet.
Completed table:
| Point | North (ft) | East (ft) | ||
| C | 406.31 | 1259.97 | 296,244 | |
| D | 235.12 | 1489.47 | 605,187 | 98,022 |
| E | 65.81 | 1126.40 | 264,839 | 358,071 |
| A | 317.89 | 942.04 | 61,996 | 636,178 |
| B | 675.32 | 1282.54 | 407,707 | 521,109 |
| C | 406.31 | 1259.97 | 850,883 | |
| sums: | 2,190,612 | 1,909,624 |
![]()
Since we carried an extra significant figure, Area = 140,490 sq ft.
c. Non-crossing traverses only
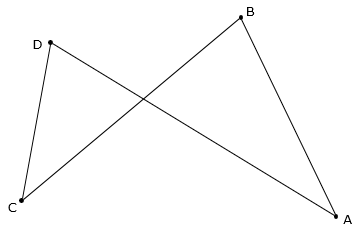
Equation H-1 will not return a correct area if a traverse crosses itself. The traverse in Figure H-3 represents the order in which the points were surveyed, traverse adjusted, etc. Applying Equation H-1 to the coordinates in their surveyed order results in an "area" of 8,412 sq ft. The area is nonsensical since the traverse doesn't have an "inside" like a non-crossing polygon.
|
|
Coordinates
Area ABCDA = 8,412 sq ft. |
|||||||||||||||
|
Figure H-3 |
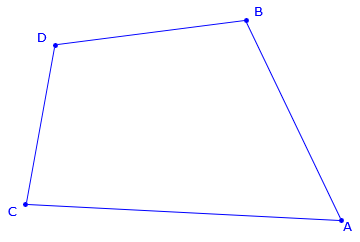
If we re-order the point list to a non-crossing perimeter, Figure H-4, the area is 70,717 sq ft.
|
|
Coordinates
Area ACDBA = 70,717 sq ft. |
|||||||||||||||
|
Figure H-4 |
Apply Equation H-1 only to a non-crossing traverse with the coordinates listed in order around the perimeter of the desired area.