2. Traverse with curves

a. Segments and sectors

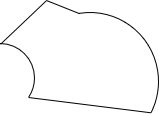
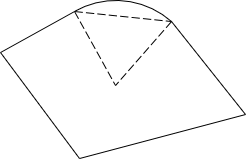
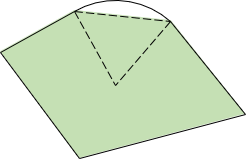
Area by coordinates is constrained to following straight lines. Where curves are involved, Figure H-3(a), the method returns an area bounded by their chords, Figure H-3(b).

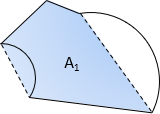
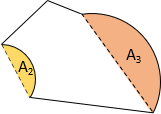
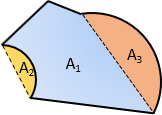
To obtain the correct area, sector or segment areas are computed and added or subtracted accordingly. For the traverse in Figure H-3(a), the two segment areas are computed, Figure H-4(a),  and one subtracted from, the other added to, the area by coordinates, Figure H-4(b).

b. Example area computation

Given the traverse in Figure H-5, determine its area.

In the table below, the points and their coordinates are in the first three columns; their cross-products are in the last two.

Point	North (ft)	East (ft)
1	500.00	1200.00		737,634
2	614.70	1249.70	624,850.	843,243
3	674.76	1347.43	828,261	892,620.
4	662.46	1552.76	1,047,730	725,778
5	467.41	1516.87	1,004,860	633,075
6	417.36	1317.39	615,766	658,696
1	500.00	1200.00	500,828
		sums:	4,491,046	4,622,300.

The area is

This is the area bounded by the chords. We must account for the segments.

Recall that the area of a segment, bounded by an arc and its chord, is

Compute the area of each segment

Arc 2-3

Arc 4-5

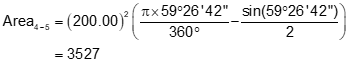
Arc 6-1

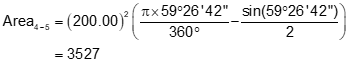
Add or subtract the segments:

Total traverse area is 68,790 sq ft.

c. Segment or sector?

Consider the curvinlinear traverse in Figure H-5:

Its area can be computed using the arc sector, Figure H-6,  

or using the arc segment, Figure H-7

Either method is fine. The only difference is that sectors require computing arc radius points, Figure H-6(a); segments do not, Figure H-7(a).