H. Area

1. Traverse with straight sides

a. Closed polygon

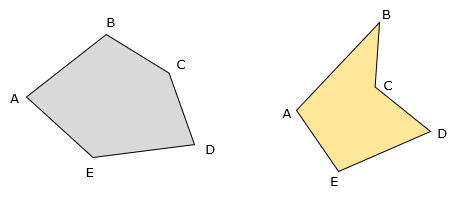
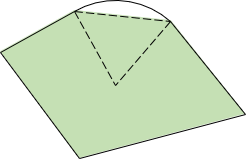
The area of any closed non-crossing polygon, Figure H-1,

can be computed using the coordinates of its verticies with Equation H-1:

This equation works for any polygon with straight sides. The more verticies, the more terms in the equation. An easy way to remember equations is graphically:

It doesn't matter:

• at which point you start
• going clockwise or counterclockwise around the polygon
• whether coordinates are East-North or North-East

The last two can affect the area's mathematical sign which is why Equation H-2 uses the absolute value.

b. Example area computation

Determine the area of the traverse in Figure H-2.

Set up the coordinates table with additional rows for first point repetition and sums and two columns for cross-products.

We'll start at point C, travel clockwise, and carry an extra significant figure to minimize cumulative rounding.

Point	North (ft)	East (ft)
C	406.31	1259.97
D	235.12	1489.47
E	65.81	1126.40
A	317.89	942.04
B	675.32	1282.54
C	406.31	1259.97
		sums:

Partial cross-products:

406.31 x 1489.47 = 605,187
235.12 x 1126.40 = 264,489
...

235.12 x 1259.97 = 296,244
65.81 x 1489.47 = 98,022
...

The units on the cross-products are square feet.

Completed table:

Point	North (ft)	East (ft)
C	406.31	1259.97		296,244
D	235.12	1489.47	605,187	98,022
E	65.81	1126.40	264,839	358,071
A	317.89	942.04	61,996	636,178
B	675.32	1282.54	407,707	521,109
C	406.31	1259.97	850,883
		sums:	2,190,612	1,909,624

Since we carried an extra significant figure, Area = 140,490 sq ft.

c. Non-crossing traverses only

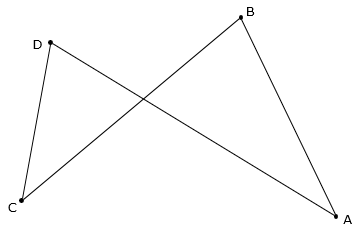
Equation H-1 will not return a correct area if a traverse crosses itself. The traverse in Figure H-3 represents the order in which the points were surveyed, traverse adjusted, etc. Applying Equation H-1 to the coordinates in their surveyed order results in an "area" of 8,412 sq ft. The area is nonsensical since the traverse doesn't have an "inside" like a non-crossing polygon.

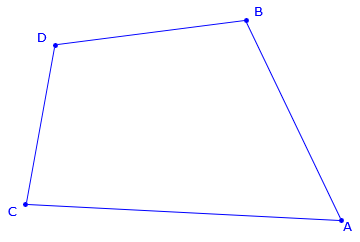
If we re-order the point list to a non-crossing perimeter, Figure H-4, the area is 70,717 sq ft.

Apply Equation H-1 only to a non-crossing traverse with the coordinates listed in order around the perimeter of the desired area.

2. Traverse with curves

a. Segments and sectors

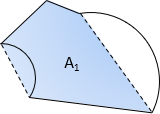
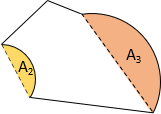
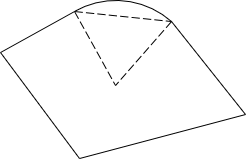
Area by coordinates is constrained to following straight lines. Where curves are involved, Figure H-3(a), the method returns an area bounded by their chords, Figure H-3(b).

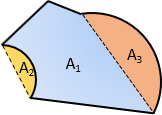
To obtain the correct area, sector or segment areas are computed and added or subtracted accordingly. For the traverse in Figure H-3(a), the two segment areas are computed, Figure H-4(a),  and one subtracted from, the other added to, the area by coordinates, Figure H-4(b).

b. Example area computation

Given the traverse in Figure H-5, determine its area.

In the table below, the points and their coordinates are in the first three columns; their cross-products are in the last two.

Point	North (ft)	East (ft)
1	500.00	1200.00		737,634
2	614.70	1249.70	624,850.	843,243
3	674.76	1347.43	828,261	892,620.
4	662.46	1552.76	1,047,730	725,778
5	467.41	1516.87	1,004,860	633,075
6	417.36	1317.39	615,766	658,696
1	500.00	1200.00	500,828
		sums:	4,491,046	4,622,300.

The area is

This is the area bounded by the chords. We must account for the segments.

Recall that the area of a segment, bounded by an arc and its chord, is

Compute the area of each segment

Arc 2-3

Arc 4-5

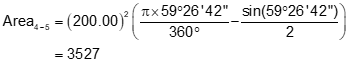
Arc 6-1

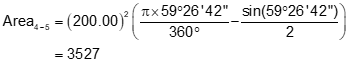
Add or subtract the segments:

Total traverse area is 68,790 sq ft.

c. Segment or sector?

Consider the curvinlinear traverse in Figure H-5:

Its area can be computed using the arc sector, Figure H-6,  

or using the arc segment, Figure H-7

Either method is fine. The only difference is that sectors require computing arc radius points, Figure H-6(a); segments do not, Figure H-7(a).