5. Intersections

a. Solution logic

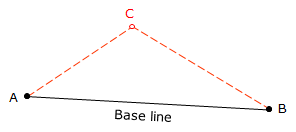
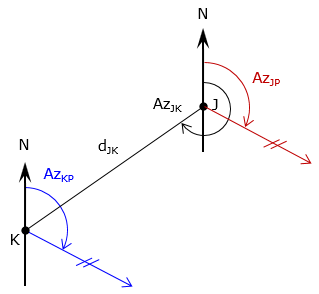
Determining the position of an unknown point requires a combination of triangle solutions along with inverse and Forward Computations. Two points with known coordinates (A and B) form one side of a triangle; inversing between them gives the length and direction of that side (the base line), Figure C-22.

Recall that three parts of a triangle, including one side, must be known to compute the other parts. Performing an Inverse Computation between the two known points fixes one side of the triangle. The other two parts come from the measurements connecting the unknown point with the base line. Using the Law of Sines or Cosines, enough additional triangle parts are computed to connect the unknown point to a known point with a distance and direction. The unknown coordinates can then be computed using a Forward Computation.

In each of the following intersection descriptions:

• Points J and K have known coordinates and define the base line
• P is the unknown point whose position is being determined 

The first step in each intersection is to inverse between points J and K to determine the base line's length and direction, thus fixing one side of the triangle and its orIentation with respect to north. The final step is a Forward Computation from one end of the base line to the unknown point. Either end of the base line may be used, computing from the other could serve as a math check.

b. Distance-distance

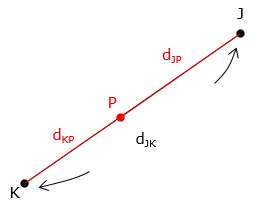
Distances from points J and K to point P (d_J and d_K) are known, Figure C-23.

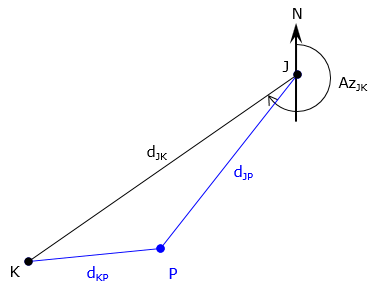Figure C-23 Distance-distance intersection

A distance-distance intersection results in two possible locations, Figure C-24.

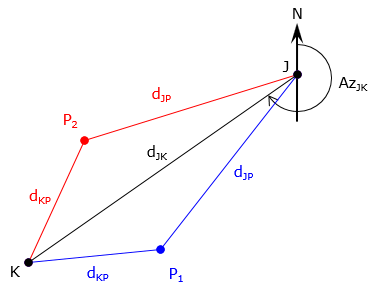Figure C-24 Two intersection points

Triangles JKP₁ and JKP₂ are mirror images: they have identical angles and distances. It's up to the surveyor to decide which point intersection point, P₁  or P₂ , to be solve. This mirror triangle situation is the reason it's difficult to determine the unknown position using simultaneous solution of Equations B-1 and B-2. The azimuth from Point J to point P is:

where J is the angle at point J between the base line and the line to point P.

It's relatively simple using triangle equations to solve for point P once we know which side of the base line it is.

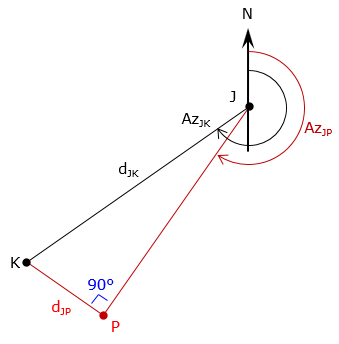
We'll solve for point P₁, Figure C-25, using a Forward Computation from point J at the base line end. We already know the distance d_JP, the direction Az_JP is needed.

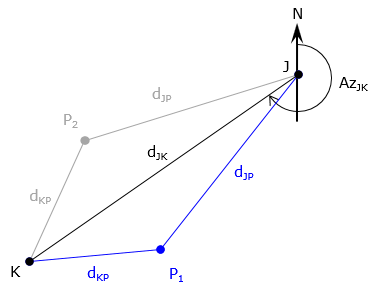Figure C-25 Distance-distance solution

Solution process

Set up the Law of Cosines and rearrange it to compute angle Q

Compute azimuth, Az_JP , from point J to the intersection point. Because point P is to the left of the base line, Equation C-7 becomes:

Forward compute from point J

Comments

What would change had we wanted the position of point P₂ instead of point P₁? Angle J would be the same except it's right of the base line instead of right. Equation C-7 would be:

In order for there to be an intersection point, (d_JP + d_KP) must be greater than d_JK. If (d_JP + d_KP) = d_JK then the intersection point is on the base line and the trianlge is a straight line, Figure C-26.

c. Direction-distance

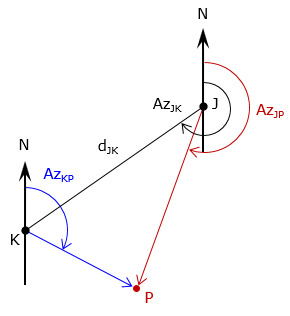
Direction from one control point (Az_JP), and distance from the other (d_KP) are known, Figure C-27.

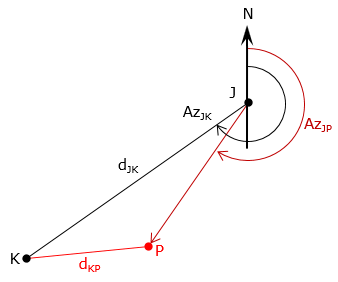Figure C-27 Direction-distance intersection

Let's determine the position of point P using a Forward Computation from point J. To do so, we need the distance d_JP. We know two sides (d_JK and d_KP) and the angle at point J which can be calculated from the two directions Az_JK and Az_JP. The simplest way to sovle d_JP is using the Law of Sines which requires the angle at K.

The solution process is:

Compute angle J by finding the difference between the base line direction (Az_JK) and direction to Point P (Az_JP). The smaller direction is subtracted from the larger. In this case:

Determine the angle at P using the Law of Sines

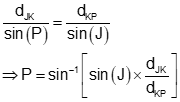
Remember that we have to be careful using the Law of Sines to compute an angle because it is ambiguous: the angle can be P or 180°-P. Figure C-28 shows the two different possible triangles. Distance d_KP can intersect the direction Az_JP at two locations.

Figure C-28 Direction-distance two intersections

We have to pick point  P₁ or  P₂ based on whether the angle P is acute (<90°) or obtuse (90°) which depends on the particular situation. 

Once the correct angle P is selected, angle K is computed from the angle condition

Distance  d_JP is determined from the Law of Sines

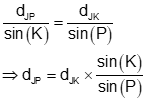
Finally, forward compute from point J to get the coordinates

Comments

If  angle P is exactly 90° a direction-distance intersection will have only a single intersection point, Figure C-29.

d. Direction-direction

Directions from points Q and R to point P (Az_Q, and Az_R) are known, Figure C-30.

Two directions intersect at only a single point so there are no multiple solutions for this method. We'll look at computing point P's coordinates as a Forward Computation from point J.

The process is:

Compute angle J as the difference between Az_JP and base line azimuth Az_JK

Compute angle K as the difference between Az_KP and base line back-azimuth Az_KJ = (Az_JK±180°)

Compute angle P using the angle condition.

Use Law of Sines to solve distance from point J to point P

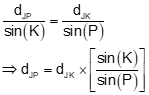
Forward compute from J

Comments

The closer Az_JP and Az_KP values are to each other, the further away their intersection will be; if the two azimuths are parallel, then no intersection is possible, Figure C-31.

Direction-direction is the only method which has a single intersection point. The other two methods involve at least one distance which result in two possible intersections.