Article Index

Page 4 of 5

4. Solving triangles

If we start with three triangle parts (including at least one distance), we can solve the reaming three parts using combinations of the Law of Sines and Law of Cosines.
Usually (although not always) there is only one way to start solving a triangle. With each additional part, there are more ways to compute remaining pieces.

Figures C-16 and C-17 show different initial angle and distance combinations and the logic to solve remaining trianle parts.

 

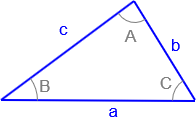
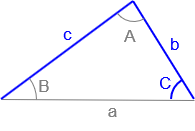
Figure C-16
Example triangle 1

 Given: Sides a, b, and c

Compute:
(1) angle A using Law of Cosines.
(2) angle B using Law of Cosines or Law of Sines.
(3) angle C using Law of Cosines or Law of Sines or angle condition.

 

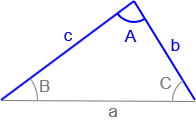
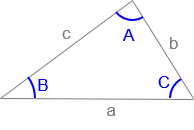
Figure C-17
Example triangle 2

 

Given: Sides b, c and included angle A.

Compute:
(1) side ausing Law of Cosines
(2) angle Busing Law of Cosines or Law of Sines.
(3) angle Cusing Law of Cosines or Law of Sines orangle condition

Try figuring out the logic to solve triangles in Figures C-18 through C-21 on your own.



Figure C-18
Example triangle 3
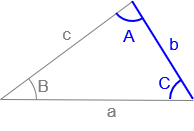
Given: Angles A, C and side b.



Figure C-19
Example triangle 4
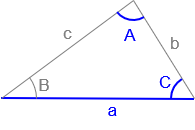
Given: Angles A, C, and side a.



Figure C-20
Example triangle 5
Given: Sides c, b, and angle C



Figure C-21
Example triangle 6
Given: Angles A, B, and C
Details
Hits: 22500