3. Trigonometric Functions
a. Sine; Law of sines
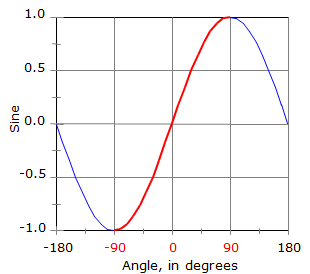
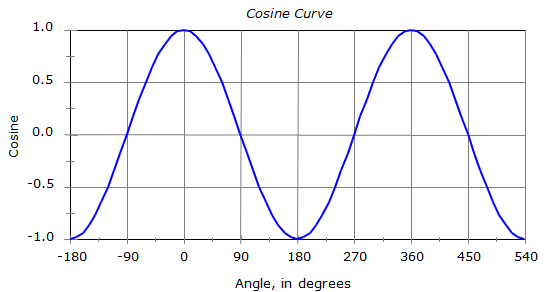
The sine of any angle falls between -1.0 and +1.0. Figure C-5 shows how angles and their sines relate. This curve repeats itself every 360°; so sin(-340°) = sin(20°) = sin(380°)...
|
|
|
Figure C-5 |
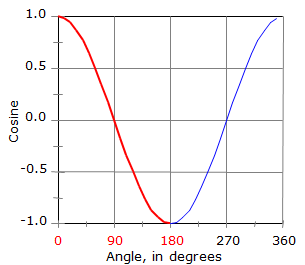
Taking the arcsine (a.k.a. inverse sine, sin-1) of a number between -1.0 and +1.0 on a calculator will always return an angle between -90° and +90°, Figure C-6.
|
|
| Figure C-6 -90° to +90° |
Table C-1 shows how angles outside ±90° relate through sin() and sin-1():
| Table C-1 | |||
| a | x = sin (a) | b = sin-1(x) | relationship |
| 30° | +0.500000 | +30° | b= a |
| 150° | +0.500000 | +30° | a = 180°- b |
| 210° | -0.500000 | -30° | a = 180°- b |
| 330° | -0.500000 | -30° | a = 360° + b |
For example sin-1(0.5) = 30° or 150° but it can only be one or the other for a particular triangle. A calculator will always return 30° even though the correct angle may be 150°. How do you know which is correct? It depends on the triangle.
To solve a triangle using the Law of Sines you must have either two angles and a side or two sides and an angle. Moreover, one known side must be opposite a known angle.
(1) Example 1
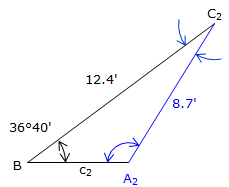
In triangle ABC, a = 12.4', b = 8.7', and B = 36°40'. Compute the remaining angles and side.
From the Law of Sines, Equation C-2:

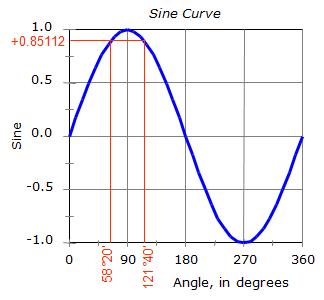
There are two angles whose sine is +0.85112: A = 58°20' and A = (180°00' - 58°20') = 121°40', Figure C-7.
|
|
|
Figure C-7 |
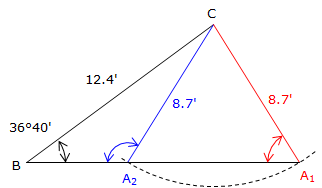
This means there are two possible triangles, Figure C-8.
|
|
|
Figure C-8 |
Consider point C as the center of an arc of radius 8.7'. This arc can intersect the remaining side at two points; A1 and A2, creating two different triangles.
Compute the remaining components for each triangle:
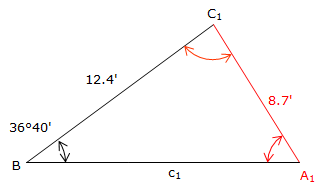
For A = 58°20', Figure C-9:
|
|
|
Figure C-9 |
From the angle condition:, Equation C-1:
![]()
Using Law of Sines:
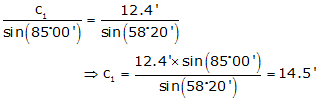
For A = 121°40', Figure C-10:
|
|
|
Figure C-10 |
From the angle condition
![]()
Using Law of Sines
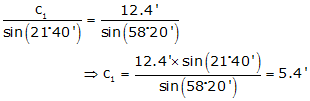
Which triangle is the correct solution? It depends on the situation. Notice that the problem statement provided numbers but not a sketch. Had a sketch been included, then the correct triangle could have been selected.
(2) Example 2
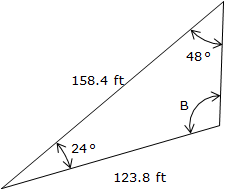
Compute angle B in the triangle of Figure C-11.
|
|
|
Figure C-11 |
The missing angle can be computed two ways:
- By Law of Sines
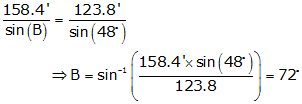
- By angle condition
![]()
As a result there are two “correct” answers for the missing angle;
sin(108°) = sin(72°) = 0.95105652
But only 108° fits both the Law of Sines and the Angle condition.
We can also visually determine which angle is correct, providing we have a reasonably drawn sketch. In Figure C-11 angle B is larger than 90° so we would select 108°.
|
Be careful when using the Law of Sines to solve for an unknown angle – there could be two possible answers only one of which will fit the particular triangle. |
b. Cosine; Law of cosines
The cosine of any angle falls between -1.0 and +1.0. Figure C-12 shows how angles and their cosines relate. This curve repeats itself every 360°; so cos(-340°) = cos(20°) = cos(380°)... The cosine curve is identical to the sine curve except its phase differs by 90°.
|
|
|
Figure C-12 |
Taking the arccos (a.k.a. inverse cosine, cos-1) of a number between -1.0 and +1.0 on a calculator will always return an angle between 0° and 180°, Figure C-13.
|
|
| Figure C-13 0° to 180° |
Table C-2 shows how angles outside ±180° relate through cos() and cos-1():
| Table C-2 | ||
| a | x = cos(a) | b = cos-1(x) |
| 60° | +0.500000 | +60° |
| 120° | -0.500000 | +120° |
| 300° | +0.500000 | +60° |
| -240° | -0.500000 | +120° |
Using the Law of Cosines will not cause an ambiguous solution as does the Law of Sines since any single angle in a triangle cannot exceed 180°.
To solve a triangle using the Law of Cosines you must have either three sides, or, two sides and an angle.
(1) Example
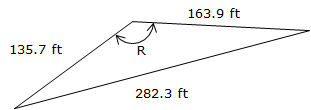
Compute the value of the angle R in the triangle of Figure C-14.
|
|
|
Figure C-14 |
From the Law of Cosines:

The Law of Cosines returns only one legitimate value when solving triangles.
c. Tangent
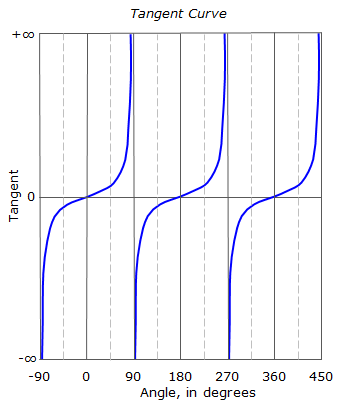
Unlike sine and cosine, the tangent of any angle not limited to the range of -1.0 to +1.0. As a matter of fact, the tangent range is ±(infinity). You can see that the tangent function plot, Figure C-15, is not sinusoidal as are the sine and cosine plots. And unlike the other two it repeats itself every 180°;
|
|
|
Figure C-15 |
The tangent curve is asymptotic at 90°, 270°, 450°, etc. Asymptotic means the curve gets close to, but never reaches, those values. Recall that tangent is sine divided by cosine. At 90°, sine = 1.0, cosine = 0.0, so tangent = 1.0/0.0 (with an identical pattern every 180°). The result of dividing by zero is infinity, hence the asymptotic plot.
Try evaluating tan(90°) on your calculator; you’ll probably get an error statement of sorts. Then try tan(89.99999°); you should get a pretty big number.
There is a Law of Tangents, but we don't generally use it to solve triangles since the Laws of Sines or Cosines are usually sufficient .