2. Plane triangle formulae

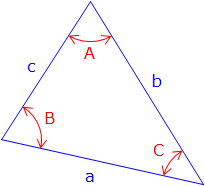
A plane triangle, Figure C-2, has six parts: three angles and three sides.

 Individual angles may be acute (<90°), right (=90°), or obtuse (>90°) with their sum exactly 180°.

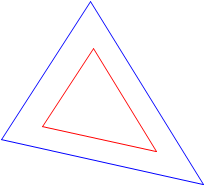
To geometrically define a triangle requires three parts, including at least one side, be fixed. Why a side? Because fixing angles alone does not constrain the size of the triangle. The two triangles in Figure C-3 are different sizes even though they have identical angles.

 Equations for triangle trigonometry are:

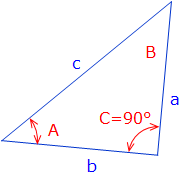
A right triangle is a special case where one angle is exactly 90°. Applying the Law of Cosines, Equation C-3, to a right triangle, Figure C-4:

Figure C-4 Right triangle

Because cos(90°) = 0 The Law of Cosines becomes the Pythagorean Theorem.

Depending on which parts of it are known the area of a triangle can be determined using one of two equations:

Using two sides and an included angle:		Equation C-4
Using three sides:		Equation C-5
where:		Equation C-6