Chapter is being updated = 10/12/24
Chapter D. Vertical Datum
1. Historical Background
a. Equipotential Surfaces
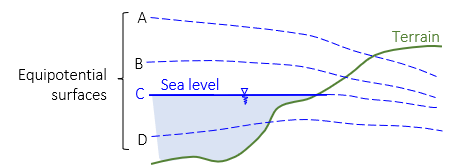
A vertical datum should be one that is a true equipotential surface. It may not be perfectly smooth, but it should represent equal force balancing. How many equipotential surfaces are there? Lots - an infinite number of them, Figure D-1.
 |
| Figure D-1 Equipotential Surfaces |
They are similar (although not identical) and have the typical oblate shape. They aren't physical surfaces, just different levels of energy.
So which one to use for a datum surface? Only one of them can be the geoid.
b. Finding Sea Level
It was mentioned earlier that a lake's surface on a calm windless day is an equipotential surface. Using a lake surface as a datum makes it relatively easy to determine elevations around its periphery. For initial vertical datum creation oceans were used - sea level would represent the geoid, Figure D-2.
 |
| Figure D-2 Sea Level Surface |
The problem with a water surface is that its height varies due to a number of factors. Chief among them are the effects of the sun and (especially) the moon. Because the moon passes over the Earth the gravitational attraction between the two changes. Their effects are threefold:
- Semidiurnal - a period of approximately half a day
- Diurnal - a period of approximately one day
- Long-period - a period of a month or more.
Other things affecting water surface height:
- Tide currents caused by the rise and fall of the tide. The currents aren't uniform, slowly increasing then decreasing causing nonlinear inertial shifts.
- During the course of a year, the Earth's distance to the Sun changes varying the gravitational attraction.
- The seas are constantly replenished by freshwater streams and rivers causing local water surface height increases.
- Meteorological conditions: wind, atmospheric pressure, etc.
In order to establish a average sea level surface, heights had to be determined at multiple locations for the Atlantic and Pacific. Tide stations were established along coastal areas surrounding the country, Figure D-3: 21 in the US and 5 in Canada by 1929. Because such a large area was covered, conditions at each tide station would differ affecting water surface height. Water height was monitored and recorded at each location over periods long enough to allow cyclic errors. These tended to average out to establish the average 0-foot elevation surface: Mean Sea Level (MSL).
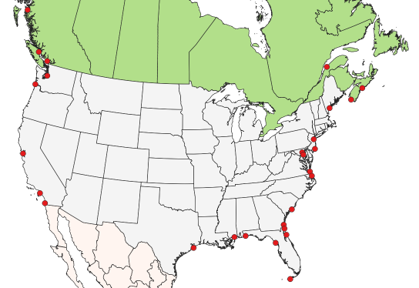 |
| Figure D-3 Tide Stations |
How long was data collected?
"A period of 19 years is generally considered as constituting a full tidal cycle, for during this period of time the more important of the tidal variations will have gone through complete cycles. It is therefore customary to regard results derived from 19 years of tide observations as constituting mean values. Hence sea level derived from 19 years of observations may be taken to constitute a primary determination and as giving accurately the datum of mean sea level."
Special Publication No. 135, Tidal Datum Planes, 1951, H.A. Marmer
Wow - 19 years.
c. Measuring Tide
Tide stations had a way to measure water surface height along with a nearby bench mark to tie to. The earliest systems required an operator to make and record readings manually. The simplest was a numbered staff, like a level rod, mounted so that water surface heights could be directly read, Figure D-4.
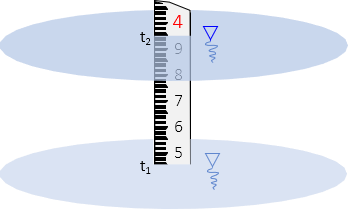 |
| Figure D-4 Staff Reading |
Another was a box gauge, Figure D-5, which had a float attached to a graduated rod. The float was inside a tube to prevent wave motion effect. Rod readings changed as the float rose and fell reacting to the water surface.
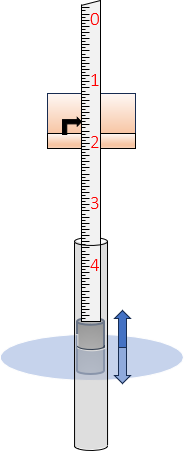 |
| Figure D-5 Box gauge |
Readings were recorded hourly, down to 15 minute intervals bracketing high and low tide events. Figure D-6 is an example of a manually recorded tide sheet.
 |
| Figure D-6 Tide Sheet |
Automatic tide gauges, Figure D-7, came into use near the beginning of the twentieth century.
 |
| Figure D-7 Automatic Tide gauge1 |
1 Special Publication No. 135, Tidal Datum Planes, 1951, H.A. Marmer
An automatic tide gauge consisted of a clock that rotated a roll of paper at a uniform rate. A pencil would trace on paper the rise and fall of a connected float. The result was a continuous tide curve from which the surface elevation could be determined at any time, Figure D-8.
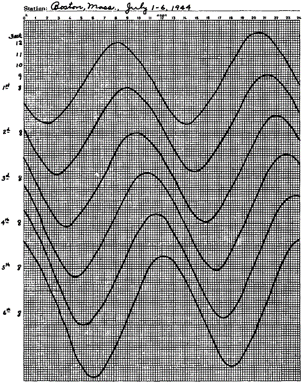 |
| Figure D-8 Tide Curve |
d. Defining the Datum
MSL at a tide station was just the average of the tide heights over the total observation period. The nearby bench mark's elevation could then be expressed in MSL at that location.
Level circuits were run between the bench marks and adjusted to create an integrated vertical control network. The network was densified and adjusted until 1929 creating these vertical datums:.
- First General Adjustment - 1899
- Second General Adjustment - 1903
- Third General Adjustment - 1907
- Fourth General Adjustment - 1912
- Sea Level Datum of 1929
Figure D-9 is a map of the First-Order leveling network making up the 1929 adjustment.
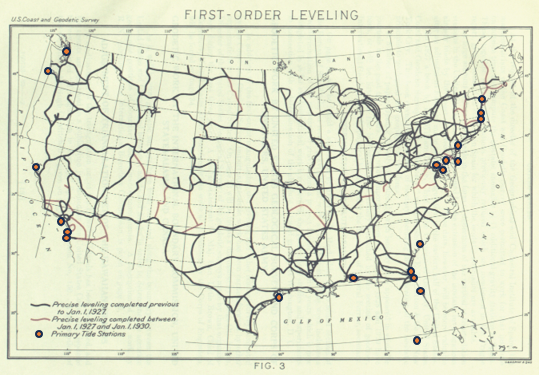 |
| Figure D-9 First-Order Networks - 19292 |
2 Special Publication No. 166 Geodetic Operations in the United States Jan 1, 1927 to Dec 31, 1929, Bowe.
The network consisted of ~100,000 bench marks and 106,724 km of leveling.
So that's how to create a Sea Level datum.
OK, so it was more complicated and involved than the brief description here, but that's the gist of it.
e. National Geodetic Vertical Datum of 1929 (NGVD 29)
What is the relationship between the Sea Level Datum of 1929 and NGVD 29?
The bench mark elevations of Sea Level Datum of 1929 were fixed and held until the decision to update the datum in the late 1970s. Many, many more control circuits were run and using increasingly more accurate equipment, Often the surveying accuracy exceeded that of the control network - accurate circuits were forced to fit less accurate control.
In its description of the National Geodetic Vertical Datum of 1929, NGS said about the Sea Level Datum of 1929:
"The datum was not mean sea level, the geoid, or any other equipotential surface. Therefore, it was renamed in 1973, the National Geodetic Vertical Datum of 1929. "
Despite all the tide gauge measurements and connecting circuits, "mean" sea level wasn't achieved and the adopted datum wasn't the geoid. A big part of the problem was that there was too much variation of "mean" sea level between all the tide stations.
So it wouldn't be correct to call the datum "Sea Level", mean or otherwise.
2. North American Vertical Datum of 1988 (NAVD 88)
a. Need for an Updated Datum
By the early 1970s the level control network had grown appreciably. But studies indicated the network was no longer meeting user needs. Although the bench marks existed on paper, many were destroyed or their height had changed due to crustal movement. Forcing contemporary level circuits to fit the datum affected new bench mark elevation accuracy.
Many destroyed bench marks were replaced and approximately 100,000 km of new lines were run. Figure D-10 shows the vertical network by 1984.
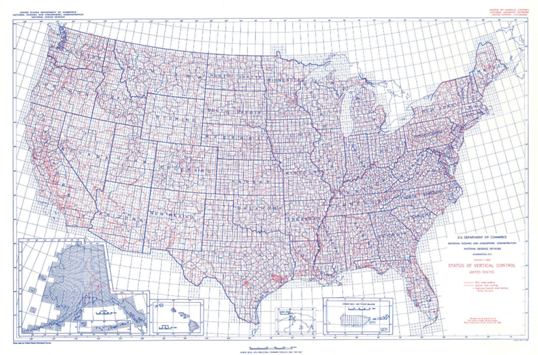 |
| Figure D-10 Vertical Networks by 1984 |
b. Datum Constraints
A primary concern for NAVD 88 was existing Federal map products in particular FEMA flood maps and USGS maps. Major or inconsistent elevation change could affect flood projections on FEMA maps which in turn affect flood plain insurance. USGS 7-1/2 minute topoquads were widely used for many applications and elevation variations would seriously impact the vertical information depicted.
To prevent warping the new datum, only one tide gauge station, Father's Point (aka, Rimouski, NSRS PID TY5255) in southeastern Canada, Figure D-11, was held fixed. It was chosen to minimize the NGVD 29 to NAVD 88 elevation differences.
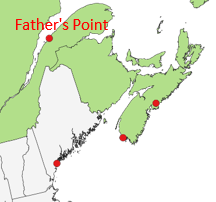 |
| Figure D-11 Father's Point |
c. Results
In Status of NAVD 88 Datum Definition, part of the collection of papers in The New Adjustment of the North American Vertical Datum, 1996, NAVD 88 Project Manager David B. Zilkowski stated:
"Finally, an important aspect to emphasize is that the bench mark height changes that will result from the NAVD 88 readjustment are primarily dues to better estimates of height differences, not because of a change in datum definition philosophy."
NAVD 88 was a refinement of NGVD 29 and, like its predecessor, was not a true geoid or sea level representation. It did, however, make the overall network more consistent.
Figure D-12 shows the elevation change from NGVD 29 to NAVD 88.
 |
| Figure D-12 Elevation Change NGVD 29 to NAVD 883 |
3 Special Publication No. 166 Geodetic Operations in the United States Jan 1, 1927 to Dec 31, 1929, Bowe.
Maximum CONUS difference is 5 ft in western Colorado. To a degree that makes sense as that area is in the Rocky Mountains (a mass anomaly) and inland from the tide stations.
d. So That's It, Right?
Well ... no. Recall that NGVD 29 wasn't the geoid and NAVD 88 was an NGVD 29 refinement so isn't the geoid either.
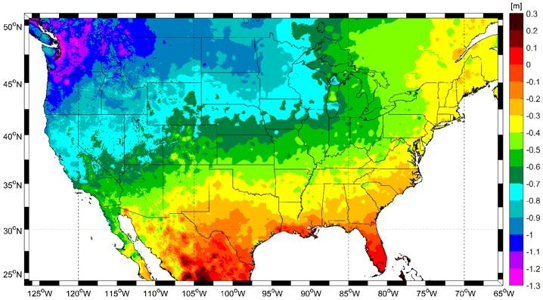
GPS, which wasn't operational when NAVD 88 was adopted, allows accurate ellipsoid height determination. Since the datum adoption, gravity measurement sophistication and accuracy has evolved. Both technologies facilitate better geoid modelling. Figure D-13 shows the approximate error in NAVD 88 based on satellite gravity data.
 |
| Figure D-13 NAVD 88 Error4 |
4 Geodesy for the Geographer : Vertical Datums for the Floodplain Manager, URISA GIS-Pro Conference, 2023, J. Jalbrzikowski
NAVD 88 appears to be tilted about a southwesterly axis.
NAVD 88's primary issues are station marks, datum adoption, adjustment control, and purpose
Station marks - Many marks/monuments are inaccessible, damaged, or missing. NGS does not have sufficient funding nor field crews to physically maintain marks.
Datum adoption - It is not a true North American datum as Canada has never adopted it. It does extend across Canada to Alaska, however there isn't much control in Alaska.
Adjustment control - to minimize overall datum-to-datum elevation changes, only a single point was used to fix the adjustment. That point was at the extreme northeast corner of the network. The further from it the faster errors accumulated.
Purpose - Rather than creating a better 0-elevation equipotential datum, NAVD 88 was intended to maintain close compatibilty with NGVD 29. It was not a true datum creation process.
So the vertical datum saga continues. Keep tuned in...
3. Orthometric Height Leveling Error
The geoid isn't the only equipotential surface - any level surface is one also.
 |
|
Fig D-14 |
The configurations of level surfaces are similar to the geoid - irregular, flattened at the poles and enlarged around the equator. Though they share similar behavior, they are not trully parallel with each other.
Let's examine a differential level circiut running from A to B, Figure D-15.
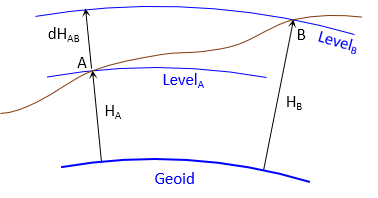 |
| Figure D-15 Differential Level Run |
The elevation difference from A to B is the difference between the BS reading sum and FS reading sum:
| |
Equation D-1 |
| |
Equation D-2 |
This is based on level surfaces being parallel, either flat planes (plane surveying) or concentric curved surfaces (geodetic surveying).
However because level surfaces are irregular and converge toward the poles the vertical spacing between them is not constant.This will introduce an error in elevations determined by differential leveling.
Over distances typically covered by differential leveling runs, the irregularity between level surfaces is generally less than their convergence. The orthometric correction, cO, is the amount the surfaces converge along the run, Figure D-16.
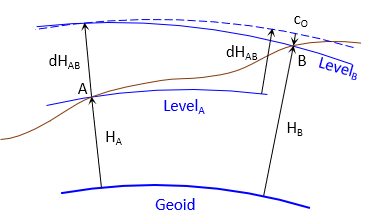 |
| Figure D-16 Converging Level Surfaces |
The ending elevation is corrected by adding the orthometric correction to it.
| |
Equation D-3 |
| Equation D-4 |
| where: | ||
| φ | Start point latitude | |
| H | Start point orthometric height | |
| Δφ' | Latitude difference, (φend-φstart); expressed in minutes | |
The orthometric correction only affects level runs having a north-south component; Δφ' is zero for strictly east-west runs.
Equation D-4 is set up to return the correct mathematical sign on the correction depending on the run direction. The units for cO are the same as those of HAvg.
Example
A differential level circuit is run from point Kollath (elev = 1139.62 ft) to point JM4. The elevation difference along the run is -379.10 ft. The approximate geodetic coordinates of both points are:
| Point | Lat | Long |
| Kollath | 42°57'28.6" W | 89°37'38.3" N |
| JM4 | 42°54'00.7" W | 89°37'51.9" N |
Determine the orthometric correction at point JM4.
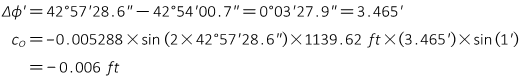
This will effect a circuit run with a three-wire level or parallel-plate micrometer. And it will have a cumulative effect on successive runs..