3. Ellipsoidal Radii
Equation H-1 requires a radius to reduce ground distance to geodetic. Because the ellipsoid is not a sphere, it does not have a single uniform radius. At each point on the ellipsoid, there are (at least) three different radii. These are dependent on the point's ellipsoid location.
a. Normal, N
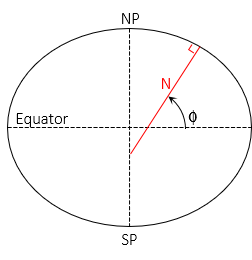
The normal is the line perpendicular to the ellipsoid surface at the observer's position, Figure H-15.
 |
| Figure H-15 Normal |
It is in the observer's meridian and extends to the semi-minor (polar) axis. The angle from the semi-major axis to the normal is the geodetic latitude, Φ.
The length of the normal varies between a at 0° lat and b at ±90° lat, Equation H-17
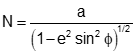 |
Equation H-17 |
b. Meridional Radius, M
The shorter an ellipsoidal arc segment, the closer it comes to being a circular arc. The meridional radius, M, is the radius of an infinitesimally short arc in the meridian at the observer's position, Figure H-16.
 |
| Figure H-16 Radius in Meridian |
Like the Normal, its length depends on geodetic latitude, Equation H-18.
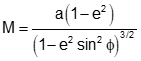 |
Equation H-18 |
c. Radius in an Azimuth, Rα
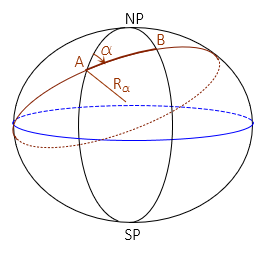
A meridian is an ellipse with the same semi-major and -minor axes as the reference ellipsoid. Connecting two points A and B not in the same meridian will create a new ellipse. If the points are at
- the same latitude, the ellipse will be at a 90° azimuth to A's and B's meridians and form a circle of fixed radius.
- different latitudes, the ellipse will be at an azimuth other than 90° (or 270°) and have semi-major and -minor axes different than the reference ellipsoid.
The radius in the direction of line AB is similar to a meridional radius except it is for a section along the new ellipse, Figure H-17 and Equations H-19 and H-20.
 |
| Figure H-17 Radius in an Azimuth |
| Equation H-19 | |
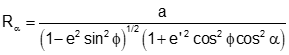 |
Equation H-20 |
d. Radius RE?
RE is typically 20,906,000 ft or 6,372,200 m which is a mean value and not dependent on latitude or direction. How does geodetic reduction using this radius compare to the others?
An example can be used to illustrate. Given:
- Latitude of point A is 41°30'00"
- Azimuth and distance to point B are 55°45'00" N and 10,000.00 ft.
- Elevations of points A and B are 900.0 ft and 800.0 ft
- Area geoid height is -32.0 m
- GRS 80 ellipsoid a = 6,378,137.0 m, e = 0.08181 919104, e' = 0.08209 44382
Compute the radii
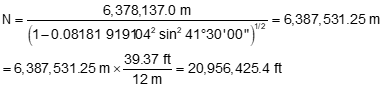

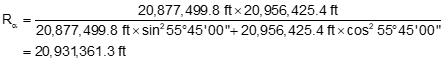
Compare to RE = 20,906,000 ft
| Radius |
Value |
diff |
diff |
| RE |
20,906,000 ft | - - | - - |
| N | 20,956,425.4 ft | +50,425.4 ft | +0.24% |
| M |
20,877,499.8 ft | -28,500.2 ft. | -0.14% |
|
Rα |
20,931,361.3 ft | +25,361.3 ft | +0.12% |
Those seem like substantial differences. How do they affect distance reduction to ellipsoid? Use each in Equation H-1 to determine the geodetic length of line AB and compare them to using RE.
| Radius |
DE |
diff |
| RE |
9,9999.6436 ft | - - |
| N | 9,9999.6445 ft | +0.0009 ft |
| M |
9,9999.6432 ft | -0.0004 ft |
| Rα | 9,9999.6441 ft | +0.0005 ft |
Despite the large radii variation, there is no significant effect on distance reduction. Even with a ground distance of 20,000 ft, the maximum difference is only 0.002 ft.
This basic analysis shows that 20,906,000 ft can be used for grid to geodetic distance reduction without affecting accuracy.