H. Ground to Grid Conversion

1. Grid Distances

a. General

In the Horizontal Datum topic, we defined three Earth surfaces and their height relationships, Figure H-1.

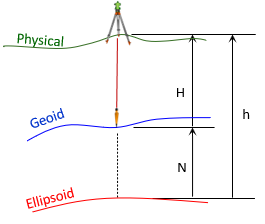Figure H-1 Surfaces and Heights

 Adding a grid introduces another surface, Figure H-2.

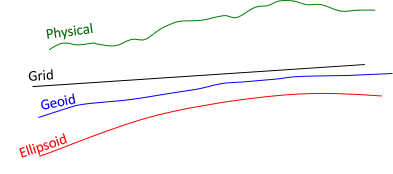Figure H-2 Inserting a Grid Surface

To convert a ground distance to grid, Figure H-3, requires going from the horizontal measurement on the physical earth, D_H, to the ellipsoid, D_E, then to the grid, D_G.

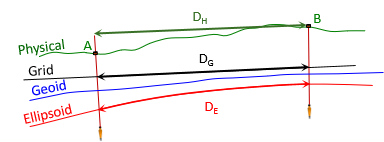Figure H-3 Ground Distance to Grid Distance

D_E is a geodetic distance since it is on the ellipsoid's surface.

b. Ground to Ellipsoid

Going from ground to the ellipsoid, Figure H-4, is done using a proportion, Equation H-1.

Figure H-4 Ground to Ellipsoid

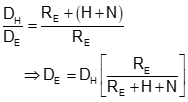Equation H-1

R_E is the ellipsoid radius. The ellipsoid has different radii depending on a line's direction and location. Because a survey line covers such a small part of the ellipsoid, its radius can be assumed constant. 6,372,200 m or 20,609,000 ft is typically used for R_E. Section 3 discusses discusses different radii and their effect on distance reduction.

The ground distance, D_H, is a straight line so D_E computed from Equation H-1 is a chord. The geodetic distance should be along the ellipsoid's surface, D_E'. The difference between the two isn't significant: the chord distance for a 20,000.0000 ft geodetic distance is 19,999.9992 ft. The distance from Equation H-1 can be used directly as the geodetic distance.

If there is a significant elevation difference between ground points and they are far enough apart, the horizontal distance between them differs based on which point it is referenced to. In Figure H-5, the distance at point B's elevation is longer than it is at point A's.

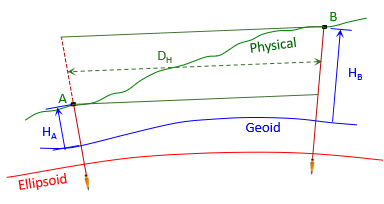Figure H-5 Average Elevation

To reduce the distance to the ellipsoid, the line's average elevation is used so Equation H-1 is modified to Equation H-2.

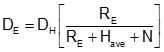Equation H-2

The term inside the brackets is called the Elevation Factor, EF, since it accounts for the orthometric and geoid heights.

The geoid doesn't vary much over a line's length so the geoid height at either end, or an average, can be used. Geoid heights over larger areas can be determined using NGS's GEOID18 Computation Tool.

The geodetic distance is independent of the grid system projection. The projection only matters when going from the ellipsoid to the grid.

c. Ellipsoid to Grid

The geodetic distance is multiplied by the scale factor to obtain the grid distance, Equation H-3.

Equation H-3

k - scale factor (aka, grid scale)

Scale is a function of the grid system location, as discussed in Chapter D. It is either computed using projection equations or obtained from the grid attributes at a control station. The latter is covered in Chapter I.

For short lines, the grid scale at either end can be used. Where the scales different significantly, their average, or weighted average (Simpson's Rule), Equation H-4, can be used.

Equation H-4

Because the ellipsoid isn't spherical, midpoint scale, k_m, is not the average of the scales at both its ends.

d. Combined Factor

The Elevation Factor and scale can be multiplied to create the Combined Factor, CF, Equation H-5. Each ground distance can be multiplied by the CF to go directly to grid, Equation H6.

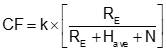	Equation H-5
	Equation H-6

Because they use average values, Equations H-5 and H-6 work best over smaller project areas where elevation changes are not excessive.