2. Projections

a. Developable Surfaces

A developable surface is one that is either flat or can be rolled out flat without distorting it. Points are projected from the ellipsoid to the surface. Because the surface is mathematically connected to the ellipsoid, distortions can be controlled by limiting the area projected or compensated by computation.

There are three primary developable surfaces, each has advantages and disadvantages for grid system construction.

(1) Plane

A plane is the simplest because it is already flat. North and East axes are added, Figure D-3, creating a coordinate system .

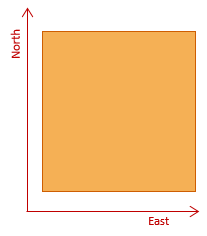Figure D-3 Plane Surface

(2) Cone

A cone can be cut from bottom to tip, rolled out flat, and a coordinate system added, Figure D-5.

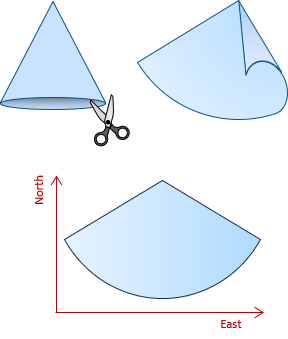Figure D-5 Conic Surface

(3) Cylinder

A cylinder can be cut axially, rolled out flat, and a coordinate system added, Figure D-4.

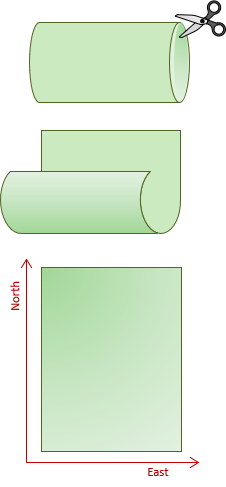Figure D-4 Cylindric Surface

b. Projection Type

Ellipsoid points can be mathematically projected to a developable surface many different ways. Although distortions are unavoidable, certain spatial conditions can be favored at the expense of others. For example, two common projection conditions are:

• Equal-Area - Area is consistent at different locations while distances and angles can change. A square in one part the projection will have the same area when moved to a different location although its shape will be distorted, Figure D-5.

• Conformal - Angular relationships around a point are maintained. A square in one part of a projection will still be a square at another location although its size will be different, Figure D-6. These are also called orthomorphic projections.

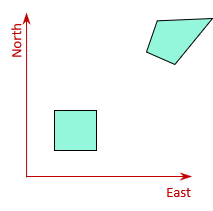Figure D-5 Equal-Area Projection	Figure D-6 Conformal Projection

Regional coordinate systems for large scale applications and used by surveyors are generally based on conformal projections.