2. Standard Error Ellipse

a. Defining the Ellipse

An adjusted point's error rectangle, Figure G-7, can be defined by the North and East uncertainties. 

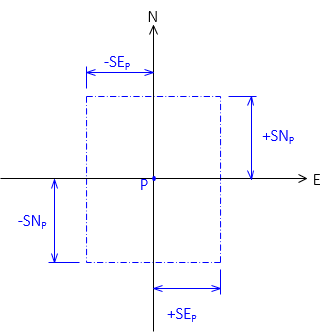Figure G-7 Error Rectangle

An error ellipse is tangent to all four sides of the error rectangle. If North and East uncertainties are the same, the error ellipse would be a circle. With differing uncertainties, there are infinite ellipses tangent to the error rectangle sides, Figure G-8. 

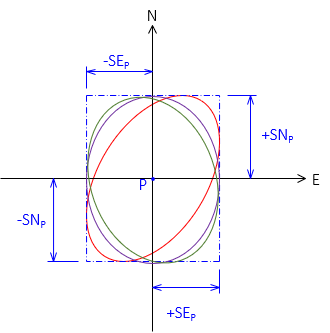Figure G-8 Many, Many Tangent Ellipses

The standard error ellipse is the one which maximizes the semi-major axis, a, and minimizes the semi-minor axis, b, Figure G-9.

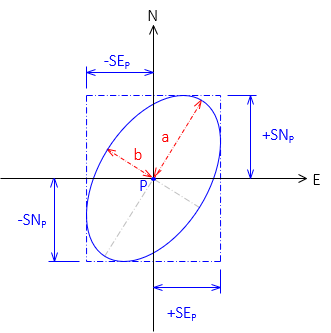Figure G-9 Standard Error Ellipse

b. Determining Parameters

The semi-major axis is the direction in which the adjusted position is weakest, it is strongest in the semi-minor direction. These directions define the auxiliary U-V axis system, Figure G-10. Az_U is the azimuth from North of the U axis.

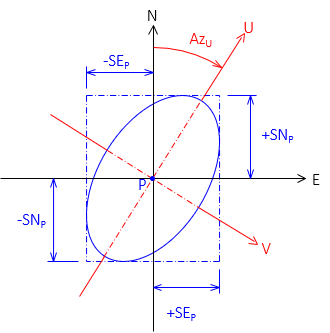Figure G-10 U-V Axis System

The covariance matrix, [Q], of a horizontal network can be viewed as a series of square 2 x 2 sub-matrices corresponding to each adjusted point, Figure G-11.

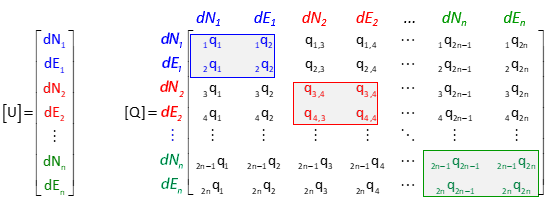Figure G-11 Unknowns and Covariance Matrices

Note: Structure of the sub-matrices depend on the coefficients arrangement in the covariance matrix. The [Q] matrix in Figure G-11 is organized by point with North then East coefficients. If  their order is reversed, or they are organized by direction instead of point (ie, all East coefficients followed by all North coefficients), the sub-matrix structures will be different. The covariance matrix organization of Figure G-11 is used in this chapter.

Figure G-12 is the sub-matrix for point i.

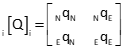Figure G-12 [Q] Sub-matrix

Diagonal elements of the sub-matrix are used to determine North and East uncertainties, Equation G-1.

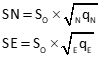Equation G-1

Off diagonal elements relate both directions for the point to each other, hence the name covariance matrix. Because [Q] is symmetric, the off diagonal elements for each point are the same.

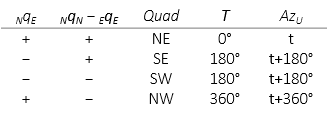
Az_U is computed from a point's covariance values , Equation G-2.

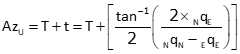	Equation G-2
T : Addend based on quadrant; Table G-1

Table G-1

Each adjusted point has a covariance matrix, [Φ], oriented to the U-V system. Figure G-13 shows the covariance matrix structure for point i.

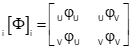Figure G-13 U-V Covariance Matrix

[Φ] diagonal elements are computed with equations G-3 through G-5.

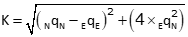	Equation G-3
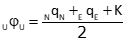	Equation G-4
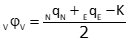	Equation G-5

Since only diagonal elements are used, the symmetric off diagonal element needn't be computed.

The standard error ellipse semi-major and -minor axis lengths are computed from the diagonal elements, Equations G-6 and G-7.

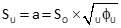	Equation G-6
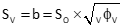	Equation G-7

c. How Confident Are We?

Standard deviations in North and East each represent an estimated 68% confidence for the respective direction. But the area of the standard error ellipse only represents about 35% confidence. That will vary somewhat based on the degrees of freedom (DF). 

Increasing the confidence interval (CI) increases the size of the standard error ellipse, Figure G-14.

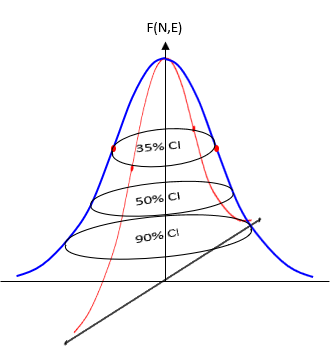Figure G-14 Confidence Intervals

To increase confidence requires use of the F Statistic (aka, F Distribution), itself in part dependent on DF. The CI at a specific percentage is computed from Equation G-8. 

	Equation G-8
F: F Statistic modifier

A common interval used by surveyors is 95%. Modifiers for 95% CI at different DF are listed in Table G-2.

Table G-2 F Statistic

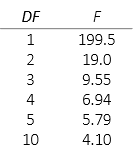Most statistic and survey adjustments textbooks have F Statistic lookup tables for other CI and DF combinations.