G. Error Ellipses

1. Introduction

Each adjusted position has uncertainty based on measurement random errors. A single dimension elevation has a vertical uncertainty, ±SElev_P, Figure G-1.

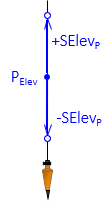Figure G-1 Elevation Uncertainty

Recall that the standard deviation of a normal distribution is approximately 68% under the symmetric bell-shaped distribution curve, Figure G-2.

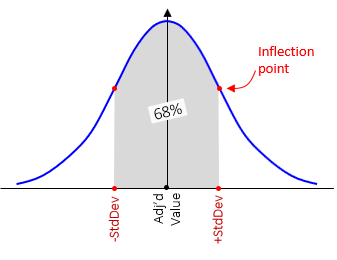Figure G-2 Normal Distribution

Standard deviation represents a 68% confidence interval. In Figure G-1, we have a 68% confidence the "true" elevation is within ±SElev_P of the adjusted value Elev_P.

A two dimension horizontal position has two uncertainties: one north, SN_P, one east, SE_P, Figure G-3.

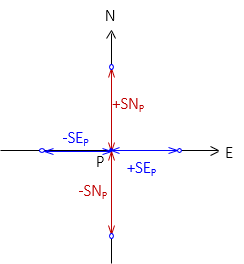Figure G-3 Horizontal Uncertainties

A horizontal position has two normal distribution curves, Figure G-4, corresponding to each direction.

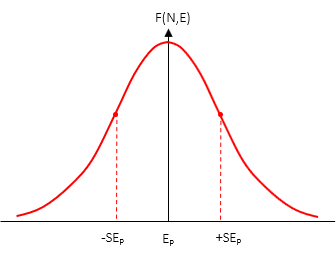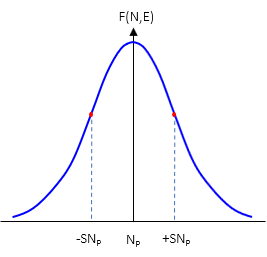(a) North	(b) East
Figure G-4 Horizontal Position Normal Curves

Even though each direction can have a different standard deviation, the two distributions are dependent on each other. They are related by the two dimensional measurements that define the position. Instead of a single simple normal distribution, the expected positional error is a bivariate normal distribution. Combining both curves, Figure G-5, creates the three dimensional bivariate distribution. 

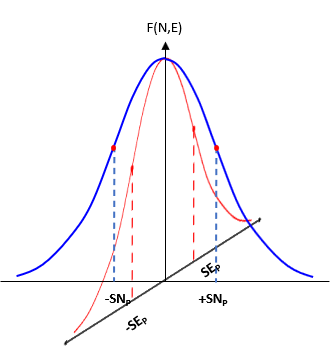Figure G-5 Bivaraiate Distribution

The perimeter trace of horizontal "slice" through the bivariate distribution is an ellipse, Figure G-6. 

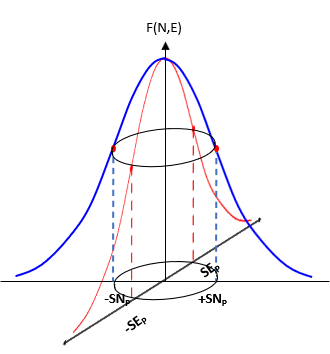Figure G-6 Error Ellipse

There are an infinite number of error ellipses, each representing a confidence region centered on the adjusted position. The standard error ellipse is the defined by the standard deviations in the North and East directions.