H. More Horizontal Examples
1. Distance Intersection
Distance intersection, also known as Trilateration, is used to determine the position of an unknown point from two or more control points. Two control points with a distance from each intersect at two possible locations. Adding a third control point and distance eliminates one of the intersections. The presence of random errors, however, means the three distances will not intersect perfectly.
Figure H-1 is shows three control points with distances that intersect at point P. Use a least squares adjustment to determine the best coordinates of point P, its uncertainty, and error ellipse.
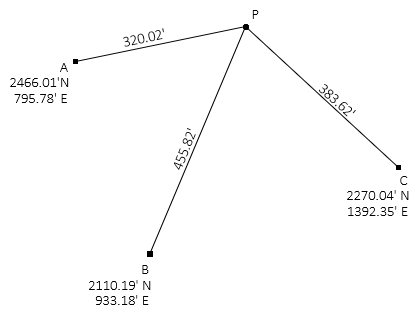 |
| Figure H-1 Distance Intersections |
Initial coordinate approximations for point P
Distance and azimuth of line BA:
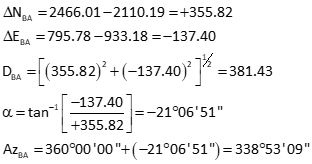
Law of Cosines to solve angle at B from A to P
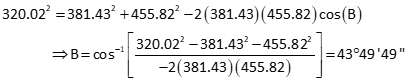
Compute azimuth from B to P
![]()
Forward computation from B to P
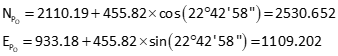
Calculate initial distances using point P's initial approximate coordinates
Because point B was used to compute point C, the computed distance is the measured distance.
![]()
Perform inverse computation to obtain distances from points A and C
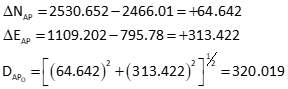

Matrix structures
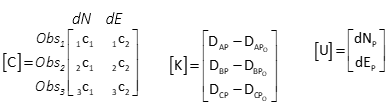
Set up the observation equations
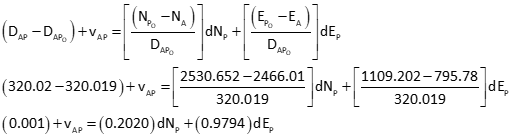
Dist AP
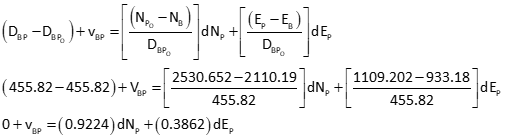
Dist BP
Dist CP

Set up matrices

Solve the matrix algorithm iteratively
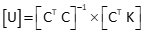
First iteration
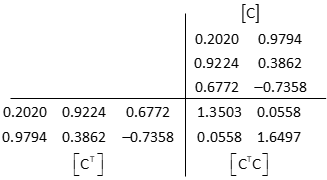
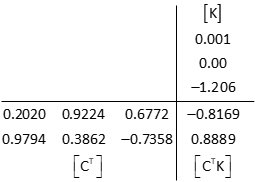
Invert the [CTC] matrix using Determinant Method

Compute coordinate updates
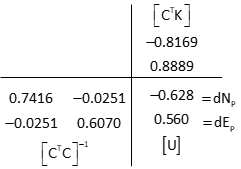
Update point P's coordinates
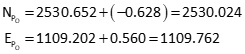
Second iteration
Update [C] and [K] matrices using the observation equations and new coordinates of point P.
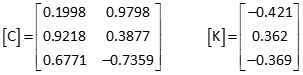
Recompute updates
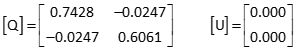
Solution converged.
Adjusted distances
Compute distance residuals from
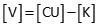
Since the last updates were zero, [C x U] is a column matrix with all elements equal to zero. Therefore:

Adjusted distances
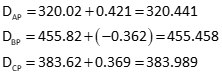
Position uncertainties

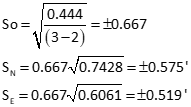
Compute error ellipse

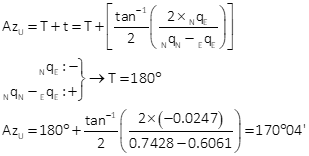
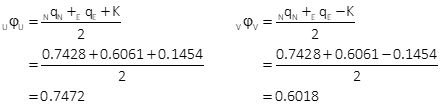
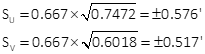
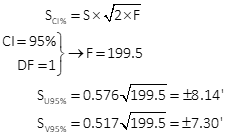
The error ellipses in Figure H-2 are magnified 25 times since they would not be visible at the drawing scale.
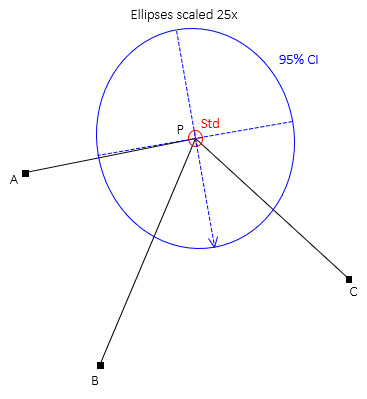 |
| Figure H-2 Standard and 95% CI Error Ellipses |
Adjustment Summary
| NP = 2530.024' ±0.574' | EP = 1109.762' ±0.519' | |
| Error Ellipse | ||
| AzU = 170°04' | ||
| SU = ±0.576' | SV = ±0.517' | |
| SU 95% = ±8.14' | SV 95% = ±7.30' | |