2. Assigning Weights

Weights can have significant impact on an adjustment. When combining multiple measurements in network adjustment, an appropriate weighting strategy should be employed. Weights can be general based on experience or detailed taking onto account multiple error sources for the type of measurement.

If a quantity is measured a sufficient number of times, the standard deviation of the measurement set can be used. How many times must a measurement be repeated for its standard deviation to be statistically significant? It depends.

Specific measurement types have particular random errors affecting their quality. These errors, described in the various Topics and Chapters on measurements, can be used to determine weights.

a. Stategies for Different Measurement Types

(1) Differential Leveling

The elevation difference between points is ( Sum_BS - Sum_FS). Weights can be assigned by:

• Number of set ups: Each time a level is set up and readings taken, there is an error potential. If the expected error is similar for each setup, then the more setups between points the greater the potential error (Error of a Series).
• Distance: As sight distances increase, there is greater reading error potential as well as random atmospheric anomolies. Even with balanced sight distances, error also increases on longer point-to-point runs, Figure E-1.

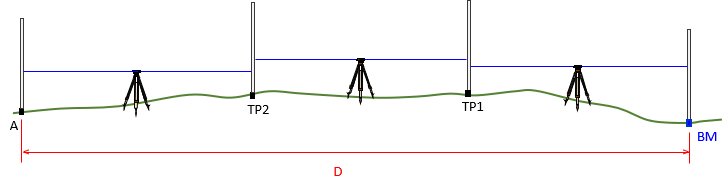Figure E-1 Leveling Error Accumulation

Weights are inversely proportional to number of setups or distance.

(2) Electronic Distance

Primary error sources in electronic distance measurement, Figure E-2, are instrument and reflector centering and the instrument's Manufacturer's Stated Accuracy (MSA).

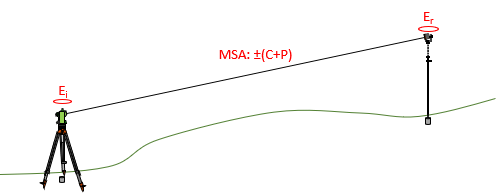Figure E-2 Electronic Distance Errors

The MSA is a random error expressed as a "constant" uncertainty along with a proportional uncertainty based on distance. It is expressed as ±(C+P), eg, ±(2 mm + 3 ppm). Equation E-2 are the combined errors,

	Equation E-2
Ei: Instrument centering error C: MSA constant P: MSA proportional Er: Reflector centering error

A distance weight is inversely proportional to the square of its error.

(3) Horizontal Angles

Angles are among the most complex measurements for which to determine a general weighting strategy. There are multiple random error sources affecting angle quality, Figure E4.

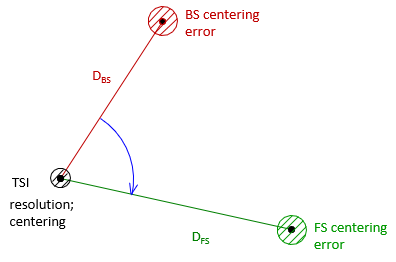Figure E-4 Angle Error Sources

 These errors are discussed in detail in Chapter D of VII. Total Station Instruments leading up to Equation D-4 of that chapter repeated here as Equation E-3.

	Equation E-3
Epr: Pointing and reading error; seconds Etsi: TSI centering error; seconds Et: Total target centering error; seconds Eang: Total angle error; seconds

Equation E-3 is deceptively subtle as each of the errors under the radical have their own equation taking into account pointings, setups, and instrument specification.

An angle's weight is inversely proportional to the square of its error.

b. Sometimes Science, Sometimes Art

A single weighting strategy for each type of measurement may not be appropriate. Network measurements, particularly horizontal and 3D, can contain a mix of instrumentation, personnel, and conditions. For example, measurements using TSIs with different pointing errors and MSAs should have their own weighting. A differential leveling circuit containing a mix of single- and three-wire observations should not use the same weighting. Even using the same equipment under similar conditions, a seasoned surveyor will probably have better measurements than a novice technician. All this, and more, must be considered for determining weights. Some can be numerically defined, others subjectively based on experience and judgement.