E. Weights
1. Introduction
The smaller the expected random error in a measurement, the higher its quality. What happens when we combine different quality measurements?
Let's say three crews measured the same distance using different equipment. Their results are:
| Method | Distance | Precision |
| Stadia | 352.11 | 1/400 |
| Steel tape | 351.92 | 1/1000 |
| Total Station Inst (TSI) | 351.35 | 1/10,000 |
What's the distance? We could use a simple average of the three distances:
![]()
Even though, by definition, the MPV is the value which minimizes the sum of the squares of the residuals, is it the best representation of the distance? Although they are of mixed quality, each measurement has the same effect on the MPV. From the precisions, it's obvious the TSI measurement is better that the others, We should allow it greater influence on the MPV. We do this by assigning weights based on measurement quality.
The weighted mean is computed using Equation E-1
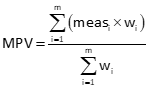 |
Equation E-1 |
|
meas: Measurement |
|
A measurement's weight is related to its error - the smaller the error, the greater the weight. Assuming measurements mistakes and systematic errors have been compensated, precision can be used as an accuracy surrogate. The weight is inversely proportional to the square of its error.Taking the inverse of each precision squared can lead to some pretty big numbers. To keep them reasonably small we can divide each by the lowest weight.
| Method | Distance | Precision | Weight | Weight |
| Stadia | 352.11 | 1/400 | 4002 | 1 |
| Steel tape | 351.92 | 1/1000 | 10002 | 6.25 |
| Total Station Inst (TSI) | 351.35 | 1/10,000 | 10,0002 | 625 |
Based on weights, the MPV is
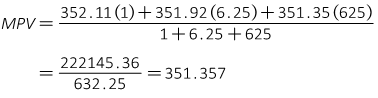
The MPV is "pulled" toward the TSI measurement since it is the highest quality.
The simple average is sometimes referred to as the unweighted mean. It can also be considered to have unit weighting, that is, the weight of each measurement is 1.