3. More Statistics

a. Propagating Error

We saw that Brute Force doesn't work when unknowns are directly connected with measurements. In the Direct Minimization method, connected unknowns appear in the same partial derivatives. Although the standard deviation of unit weight, S_o, for overall adjustment can be computed in both methods, neither allows easy determination of the expected quality of their individually adjusted values.

The Matrix method allows S_o to be propagated into the adjusted values with the covariance matrix, [Q] . It is used to compute expected standard errors of adjusted unknowns or adjusted observations. The corresponding unknowns for the [Q] matrix in Figure D-1 are u₁, u₂, u₃, ... u_n. 

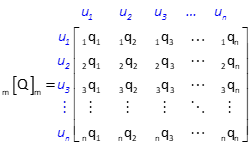Figure D-1 Covariance Matrix

b. Standard Errors of Adjusted Values

Each covariance matrix diagonal element is unique to one of the unknown quantities and is used to compute its expected error, Equation D-3.

Equation D-3

c. Standard Errors of Adjusted Observations

An adjusted observation is computed by adding its residual to the original observation, Equation D-4.

	Equation D-4
i: observation number vi: ith element of V matrix

Uncertainties of the adjusted observations are related by the observation coefficients, covariance matrix, and S_o. The cofactor matrix, [Σ], is a product of the [C], [Q], and [C^T] matrices, Equation D-5.

Equation D-5

The size of the cofactor matrix is m x m, Figure D-2, so it can be quite large if there are many observations.

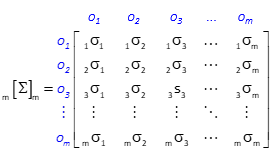Figure D-2 Cofactor Matrix

 The standard error of an observation is computed with Equation D-5.

	Equation D-5
iσi :  Diagonal element of [Σ] for observation i

Because only a diagonal element is needed, the computations can be reduced somewhat. Each row of the [C] matrix corresponds to a particular observation. Because [C^T] is the transpose of [C], each of its columns correspond to the same observations, Figure D-3.

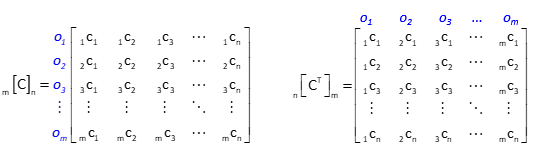Figure D-3  [C] and [CT] Matrices

An observation's [Σ] matrix diagonal element can be computed using its [C] row and [C^T] column with the [Q] matrix, Equation D-6.

	Equation D-6
i: observation number ic.. : ith row of [C] matrix :cTi : ith column of [CCT] matrix

Equation D-7 is Equations D-5 and D-6 combined.

Equation D-7