3. Refraction
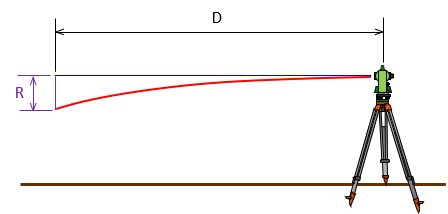
Atmosphere has density and an electromagnetic energy ray passing through it will be bent. That includes the LoS through an instrument's telescope. The denser the atmosphere, the more the LoS is bent.
Atmosphere is generally densest near the ground and decreases with elevation. When sighting longer distances, our LoS starts at the instrument's density condition and is bent downward as it progresses towards the target, Figure I-4
|
|
| Figure I-4 Refraction |
The amount the LoS refracts from the straight line is not linear: at 200 feet it is not twice the refraction at 100 feet. Over short distances, the atmosphere density distribution is relatively uniform. At longer distances that is probably not true. Solar heating and weather fronts can cause anomalous atmospheric pockets disrupting the otherwise smoothly refracted path. Local heat waves, even over short distances, can randomly affect LoS displacements.
Basically, getting a strong handle on how refraction behaves is relatively difficult. To simplify the situation, somewhat, its overall effect on readings is relatively small, considerably smaller than curvature. In most computations, refraction error is taken as a percentage of earth curvature. It varies from 17% at sea level (dense atmosphere) to 7% in mountainous areas (less dense) with 14% used as a common overall factor. It's computed using Equation I-4; because the LoS is depressed, the equation is negative.
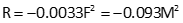 |
Equation I-4 |
D: Straight line distance from instrument to target; measured
R: Earth radius; 20,906,000 ft or 6,372,200 m
Table I-2 shows the refraction displacement at select distances from 100 to 5000 ft.
| Table I-2 | |
| Distance | R; feet |
| 100 | 0.000 |
| 200 | 0.000 |
| 300 | 0.000 |
| 400 | -0.001 |
| 500 | -0.001 |
| 1000 | -0.003 |
| 2000 | -0.013 |
| 4000 | -0.053 |
| 5000 | -0.083 |