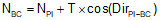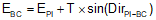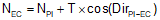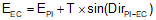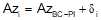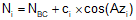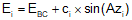4. Curves and Coordinates
a. Coordinate Equations
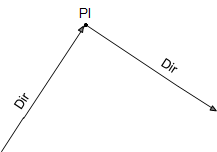
Equations C-16 and C-17 are general equations for computing coordinates using direction and distance from a known point, Figure C-26.
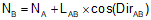 |
Equation C-16 | |
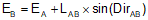 |
Equation C-17 |
 |
| Figure C-26. Coordinate Computation |
Direction (Dir) may be either a bearing or azimuth.
Curve point coordinates can be computed using these equations from a base point. Since the radial chord method uses the BC as one end of all the chords, it can also be used as the base point for coordinate computations.
b. Computation Process
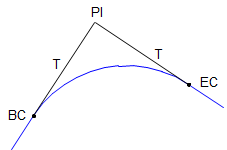
Assuming we start with the tangents and PI, then fit a curve, the general process is as follows:
|
Figure C-27 |
The original tangent lines have directions; PC has coordinates. | ||||||||||
|
Figure C-28 |
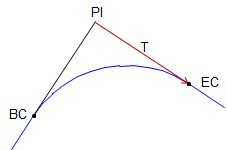
A curve is fit to the tangents. End points are at distance T from the PI along the tangents. |
||||||||||
|
Figure C-29 |
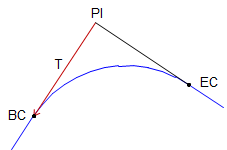
Compute coordinates of BC using back-direction of the tangent BC-PI and T.
|
||||||||||
|
Figure C-30 |
Compute coordinates of EC using direction of the tangent PI-EC and T. These will be use for a later math check.
|
||||||||||
|
Figure C-31 |
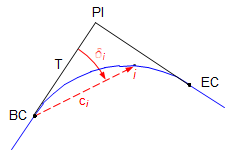
Use a curve point's deflection angle to compute the direction if its radial chord from the BC.
δ is positive for right deflections, negative for left.
|
c. Example
Continuing with the previous example problem.
Summary of given and computed curve data:
| Δ = 55°00'00" | R = 500.00 ft | |
| D = 11°27'33.0" | L = 479.965 ft | T = 260.284 ft |
| LC = 461.749 ft | E = 63.691 ft | M = 56.494 ft |
| Point | Station |
| PI | 25+00.00 |
| BC | 22+39.716 |
| EC | 27+19.681 Bk = 27+60.284 Ah |
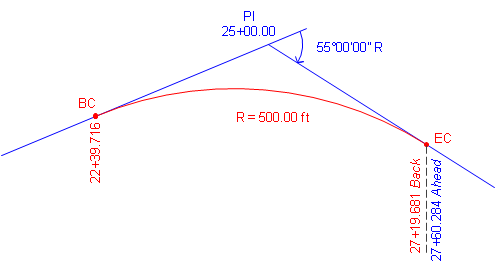
Additional information: Azimuth of the initial tangent is 75°40'10"; coordinates of the PI are 1000.00 N, 5000.00' E.
Compute coordinates of the BC:
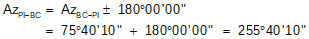
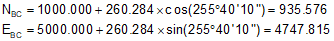
Compute the coordinates of the EC:
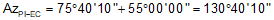
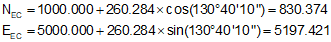
Set up Equatons C-21 through C-24 for this curve.
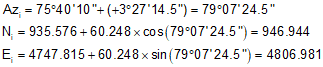
This is the Radial Chord table computed previously:
| Curve Point | Arc dist, li, (ft) | Defl angle,δi | Radial chord, c | |
| EC | 27+19.681 Bk | 479.965 | 27°30'00.0" | 461.748 |
| 27+00 | 460.284 | 26°22'20.4" | 444.203 | |
| 26+00 | 360.284 | 20°38'33.9" | 352.540 | |
| 25+00 | 260.284 | 14°54'47.4" | 257.355 | |
| 24+00 | 160.284 | 9°11'01.0" | 159.599 | |
| 23+00 | 60.284 | 3°27'14.5" | 60.248 | |
| BC | 22+39.716 | 0.000 | 0°00'00.0" | 0.000 |
Add three more columns for direction and coordinates:
| Curve Point | Azimuth, Azi | North, Ni | East, Ei | |
| EC | 27+19.681 Bk | |||
| 27+00 | ||||
| 26+00 | ||||
| 25+00 | ||||
| 24+00 | ||||
| 23+00 | ||||
| BC | 22+39.716 | |||
Complete the table using the three equations for this curve
At 22+39.716, we're still at the BC so the coordinates don't change.
At 23+00:
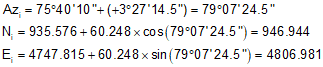
At 24+00:
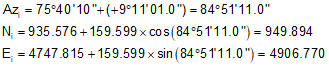
and so on for the rest of the curve points.
The completed curve table is:
| Curve Point | Azimuth, Azi | North, Ni | East, Ei | |
| EC | 27+19.681 Bk | 103°10'10.0 | 830.375 | 5197.419 |
| 27+00 | 102°02'30.4" | 842.904 | 5182.244 | |
| 26+00 | 96°18'43.9" | 896.816 | 5098.218 | |
| 25+00 | 90°34'57.4" | 932.959 | 5005.157 | |
| 24+00 | 84°51'11.0" | 949.894 | 4906.770 | |
| 23+00 | 79°07'24.5" | 946.944 | 4806.981 | |
| BC | 22+39.716 | 75°40'10" | 935.576 | 4747.815 |
Math check: the coordinates computed for the EC in the table should be the same as the EC coordinates computed from the PI. Within rounding error, that's the case here.
d. Summary
The radial chord method lends itself nicely to computing curve point coordinates. The computations are not complex, although they are admittedly tedious.
Once coordinates are computed, field stakeout is much more flexible using Coordinate Geometry (COGO).