3. Radial Chord Method
a. Circular Geometry
For any circular arc, the angle between the tangent at one end of the arc and the chord is half the arc's central angle, Figure C-21.
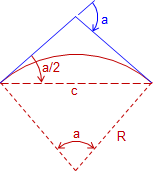 |
| Figure C-21 Deflection angle |
Angle a/2 is the deflection angle from one end of the arc to the other. The chord's length is computed from:
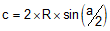 |
Equation C-10 |
In terms of the degree of curvature, Figure C-22:
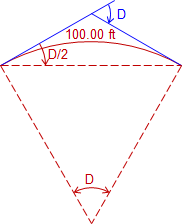 |
| Figure C-22 Full station deflection angle |
The deflection angle for a full station is half the degree of curvature. Since the deflection angle is D/2 and it occurs over a 100.00 ft, the deflection rate can be computed from:
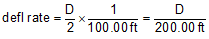 |
Equation C-11 |
Extending this geometry to the entire curve, Figure C-23, the total deflection angle at the BC from the PI to the EC is Δ/2.
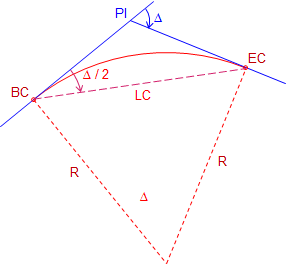 |
| Figure C-23 Deflection angle for entire curve |
Since the deflection angle occurs across the curve's length, the deflection rate can also be written as Equation C-12.
 |
Equation C-12 |
b. Radial chords
One way to stake a horizontal curve is by the radial chord method, Figure C-24.
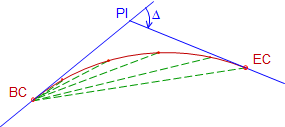 |
| Figure C-24 Radial chord method |
An instrument is set up on the BC and the the PI is used as a backsight. Then to stake each curve point, an angle is turned and distance measured. For each curve point, we need to compute its deflection angle from the tangent and chord distance from the BC.
The deflection angle to any point i on the curve, Figure C-25, can be computed from Equation C-13.
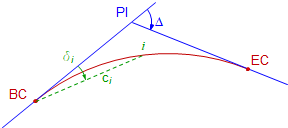 |
| Figure C-25 Deflection angle and radial chord |
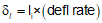 |
Equation C-13 |
li is the arc distance to the point from the BC and is computed using Equation C-14.
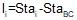 |
Equation C-14 |
Equation C-10 can be re-written using the deflection angle:
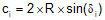 |
Equation C-15 |
Using Equations C-13 to C-15, the deflection angle and distance to any curve point from the BC can be computed.
c. Example
Determine the radial chord stakeout data at full stations for the example from Section 2.d.
Summary of given and computed curve data:
| Δ = 55°00'00" | R = 500.00 ft | |
| D = 11°27'33.0" | L = 479.965 ft | T = 260.284 ft |
| LC = 461.749 ft | E = 63.691 ft | M = 56.494 ft |
| Point | Station |
| PI | 25+00.00 |
| BC | 22+39.716 |
| EC | 27+19.681 Bk = 27+60.284 Ah |
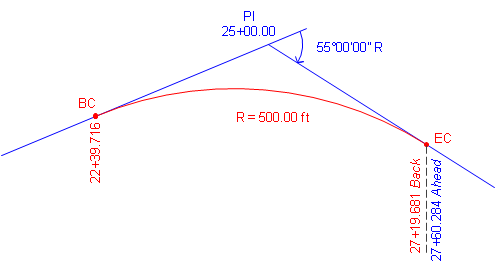
Use Equation C-11 to compute the curve's deflection rate:
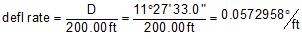
Set up Equations C-13, C-14, and C-15 for the curve:

Set up the Curve Table:
| Curve Point | Arc dist, li, (ft) | Defl angle,δi | Radial chord, ci | |
| EC | 27+19.681 Bk | |||
| 27+00 | ||||
| 26+00 | ||||
| 25+00 | ||||
| 24+00 | ||||
| 23+00 | ||||
| BC | 22+39.716 | |||
Solve the three equations for each curve point and record the results in the table.
At 22+39.716, we're still at the BC so all three entries are zero.
At 23+00:
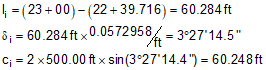
And so on until the table is complete.
| Curve Point | Arc dist, li, (ft) | Defl angle,δi | Radial chord, ci | |
| EC | 27+19.681 Bk | 479.965 | 27°30'00.0" | 461.748 |
| 27+00 | 460.284 | 26°22'20.4" | 444.203 | |
| 26+00 | 360.284 | 20°38'33.9" | 352.540 | |
| 25+00 | 260.284 | 14°54'47.4" | 257.355 | |
| 24+00 | 160.284 | 9°11'01.0" | 159.599 | |
| 23+00 | 60.284 | 3°27'14.5" | 60.248 | |
| BC | 22+39.716 | 0.000 | 0°00'00.0" | 0.000 |
Math checks:
Arc distances between successive full stations differ by 100.00 ft.
At the EC:
Arc distance should equal the curve length
Defl angle should equal Δ/2
Radial chord should equal Long Chord
The difference between deflection angles at successive full stations should be D/2.
These checks have been met.
Remember that we carried additional decimal places to minimize rounding errors. Rounding can become quite pronounced for long flat curves so computation care must be exercised. Once the table has been computed, the final values can be shown to reasonable accuracy levels. For example, distances can be shown to 0.01 ft and deflection angles to 01".
d. Summary
Computing and staking curve points by the radial chord method is simple and straightforward. Using the curve equations, any point on the curve can be computed and staked, not just those included in the curve table.
However, in the field, it may not be the most efficient way to stake a curve using modern instrumentation, particularly with long curves which may have chords thousands of feet long at very small deflection angles. Most contemporary survey computations and fieldwork use coordinates giving greater stakeout flexibility. While the radial chord method may not be used for stake out, it is well adapted to coordinate computations as we'll see in the next section.