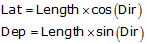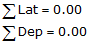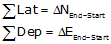3. Traverse Closure; Adjustment
a. Similarities; Differences
Latitudes and departures are computed same as those for a loop traverse:
|
|
Equations D-1 and D-2 |
Where the two differ is in how their closure is determined and adjustments made.
On a loop traverse, the closure condition is:
|
|
Equations D-3 and D-4 |
But because a link traverse does not close back on itself, that condition does not apply. Instead, we need to know the location, relative or absolute, of the traverse's end points.
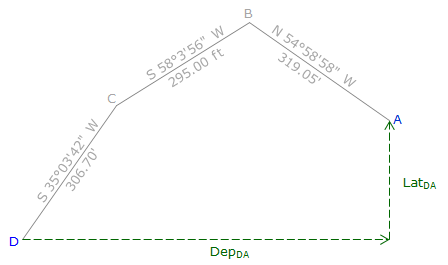
If we know the relative location, Figure H--12,
|
|
|
Figure H-12 |
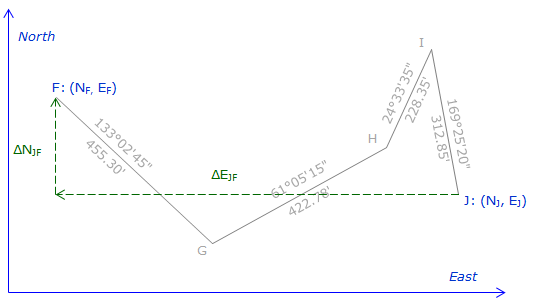
If we have coordinates of the endpoints, Figure H-13,
|
|
|
Figure H-13 |
the closure condition is
|
|
Equations H-1 and H-2 |
The latitude and departure errors would be a result of how well the closure condition was met. Linear closure and precision would be determined just as for a loop traverse.
b. Example
Given the link traverse in Figure H-14 with adjusted directions and known end point coordinates:
|
|
|
Figure H-14 |
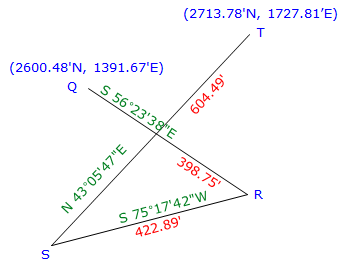
(1) Compute latitudes and departures
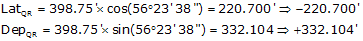
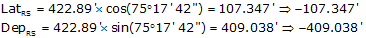
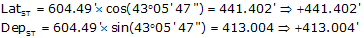
| Line | Direction | Length | Lat | Dep |
| QR | S 56°23'38"E | 398.75' | -220.700' | +332.104' |
| RS | S 75°17'42"W | 422.89' | -107.347' | -409.038 |
| ST | N 43°05'47"E | 604.49' | +441.402' | +413.004' |
| sums: | 1426.13' | +113.355' | +336.070 |
(2) Compute closure and precision
From the coordinates
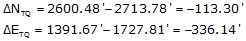
The closure and precision are
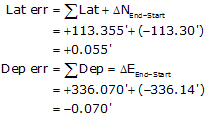
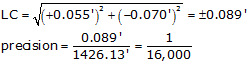
(3) Adjusting by the Compass Rule
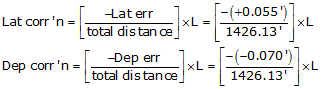
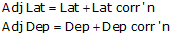
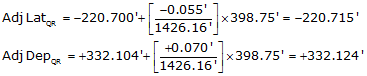
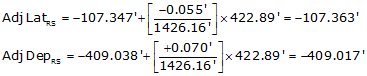
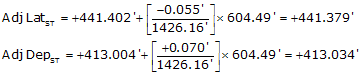
| Line | Direction | Length | Lat | Dep | Adj Lat | Adj Dep |
| QR | S 56°23'38"E | 398.75' | -220.700' | +332.104' | -220.715' | +332.124' |
| RS | S 75°17'42"W | 422.89' | -107.347' | -409.038 | -107.363' | -409.017' |
| ST | N 43°05'47"E | 604.49' | +441.402' | +413.004' | +441.379' | +413.034' |
| sums: | 1426.13' | +113.355' | +336.070 | +113.301' | +336.141' | |
| check | check |
Adjusted lengths and directions would be computed the same as for a loop traverse, as would coordinates.