2. Angles; Misclosure & Adjustment

a. Concept

Because a link traverse doesn't close back on itself there are is no interior angles sum against which to check.

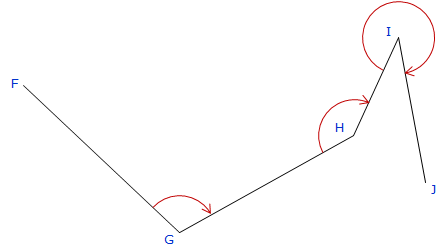
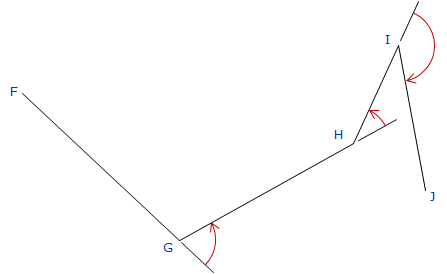
Typically, angles on a link traverse are either consistently turned in the same direction, Figure H-3, or deflection angles are measured, Figure H-4.

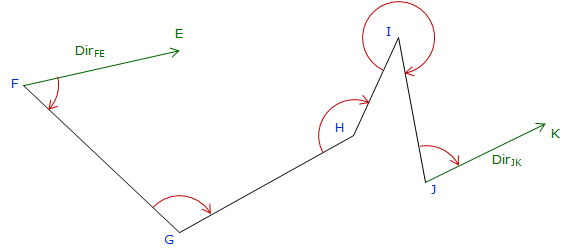
In order to check angle closure, the traverse must start and end with known directions, Figure H-5.

To determine and distribute the angular misclosure is a two step process

1. Using the start direction and measured angles, compute the raw direction of each line. The difference between the computed and known end directions is the angular misclosure.

2. Using whatever desired correction method, correct each raw direction for the misclosure.

The known directions can be explicit (bearing or azimuth) or be computed from coordinates.

If one or other direction at the traverse ends is missing then angle misclosure and adjustment cannot be done. This step would be skipped and the process would continue with latitude and departure computations.

b. Examples

(1) Link Traverse 1

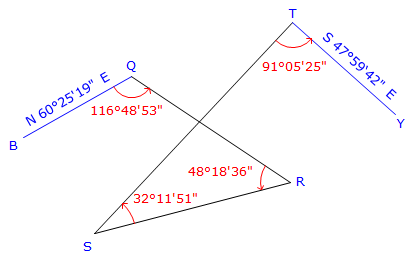
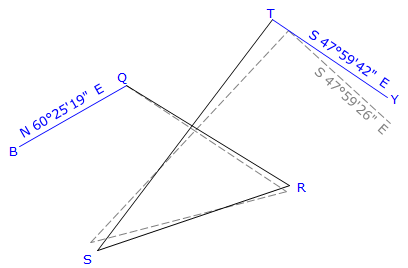
The crossing traverse in Figure H-6 begins and ends on known bearings and uses angles measured to the left at each point.

Starting with Brng_QB, the remaining bearings are computed using the measured angles. The angular misclosure is the difference between computed and known bearings of line QB.

Compute raw bearings

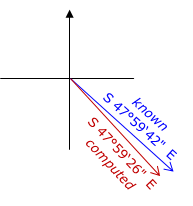
Compare computed and known bearings of line TY, Figure H-7.

Angular misclosure = 47°59'42" - 47°59'26" = +0°00'16"

Since there are four angles, each would be corrected by 0°00'04". We could either:

Apply the correction to each angle and then then recompute the directions, or,

Apply the correction to each direction.

We'll demonstrate the latter method.

From Figure H-7, it can be seen that each direction must be rotated counter-clockwise. The first direction would be rotated 0°00'04", the second 0°00'08", and so on, Figure H-8.

Because bearings are used, we need to examine which quadrant they fall in to determine if the bearing angle increases or decreases. Based on Figure H-7, bearing angles in the SE and NW quadrants will be increased, those in the NE and SW decreased.

If you compute the new angles between the adjusted bearings, you would find that each angle is increased by 0°00'04".

(2) Link Traverse 2

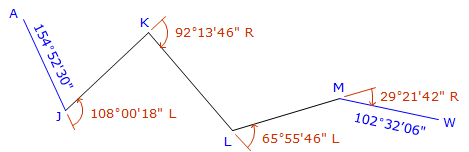
The link traverse in Figure H-9 starts and ends on known azimuths and uses deflection angles measured at each point.

As with the bearing example, the angular misclosure is the difference between the computed and known direction of the last line.

Compute raw azimuths

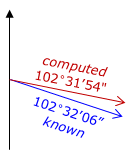
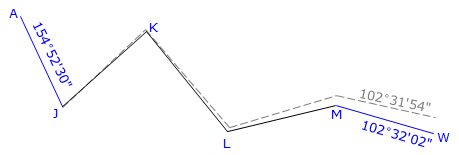
Compare the computed and known direction of line MW, Figure H-10.

Angular misclosure = 102°32'06" - 102°31'54" = +0°00'12"

Since there are four deflection angles, each would be corrected by 0°00'03". We could either:

Apply the correction to each deflection angle and then then recompute the directions, or,

Apply the correction to each direction.

We will again apply the corrections directly to the azimuths. The raw direction must be rotated clockwise into the known direction. Unlike bearings, we don't need to worry about quadrants for azimuth corrections - each azimuth is corrected in the same direction, Figure H-11.

 Because the computed closing direction must be rotated clockwise into the known closing direction, each raw azimuth will have a clockwise correction applied.