b. Inverse Computation

An inverse computation is used to determine the distance and direction between two coordinate pairs. The computations involved are basically the same as those for determining a line's new length and direction from its adjusted lats and deps.

For the traverse shown in Figure F-7, how would we determine the length and direction of the line from point T to point R?

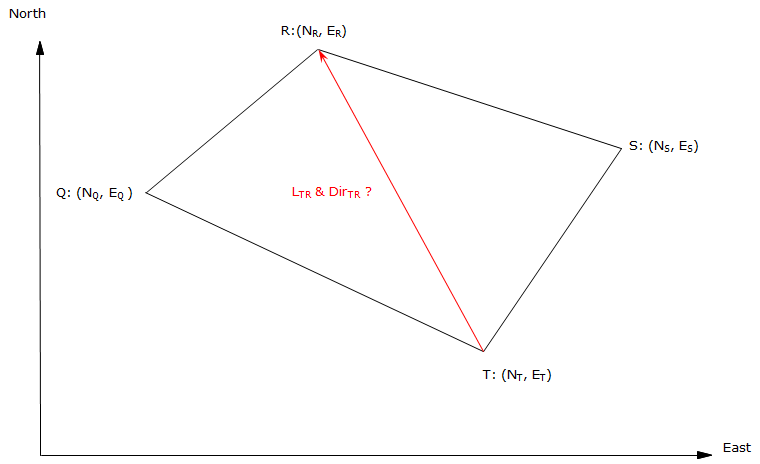Figure F-7 Length and Direction Between Nonadjacent Points

Knowing the coordinates of the two points, we can determine the latitude and departure of the line from the coordinate differences, Figure F-8.

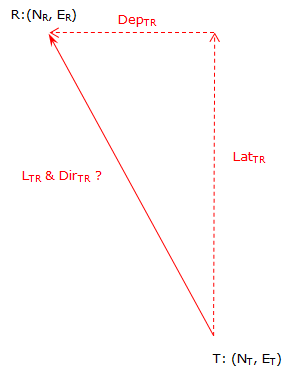Figure F-8 Length and Direction from Coordinates

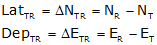Equations F-5 and F-6

Note that the differences are the To point values minus the From point values.

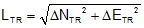		Equation F-7
and
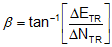		Equation F-8
where
-90° ≤ ß ≤ 90°

The mathematic signs on the coordinate differences determine the direction quadrant, Figure F-9.

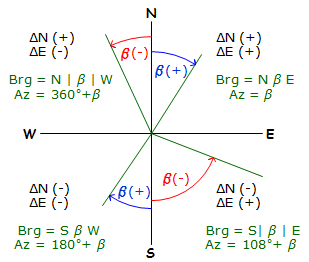Figure F-9 Converting ß to a Direction

If X and Y coordinates are used, remember that Y corresponds to N and X corresponds to E.