2. Coordinates Computations

a. Forward Computation

A forward computation uses a starting coordinate pair along with a distance and direction to determine another coordinate pair.

In Figure F-5, starting with coordinates at P, compute the coordinates at Q.

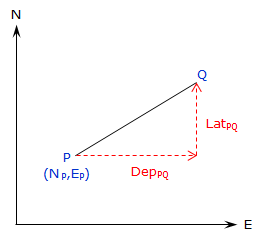Figure F-5 Forward Computation

Using Equations D-1 and D-2, the latitude and departure of the line are:

  To compute X and Y coordinates:

To compute N and E coordinates:

For a complete traverse, Figure F-6:

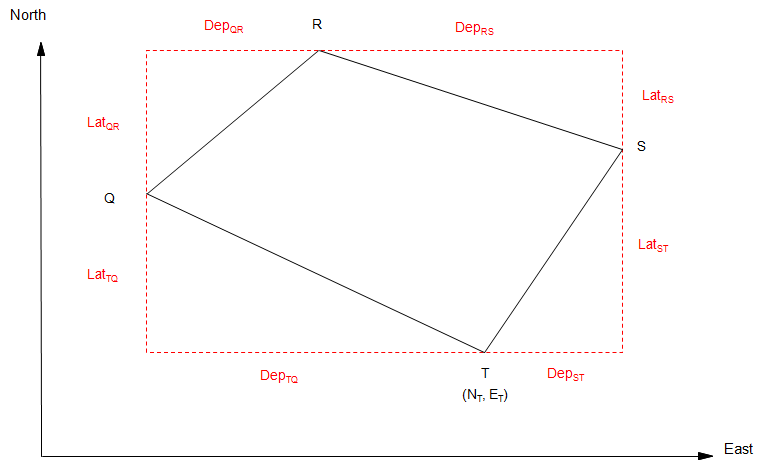Figure F-6 Coordinates Around a Loop Traverse

Starting with known coordinates at T (N_T, E_T) and applying Equations F-3 and F-4 around the traverse:

Compute coordinates of Q: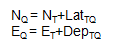
Compute coordinates of R: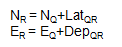
Compute coordinates of S: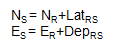
Compute coordinates of T: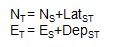

Computing back into T gives a math check: the end coordinates should be the same as the start coordinates.

In order for the math check to be met, adjusted lats and deps must be used.

Where do the start coordinates come from? They can be assumed or they could be from a formal coordinate system. We'll discuss formal coordinate systems in a later topic.