3. Intersections

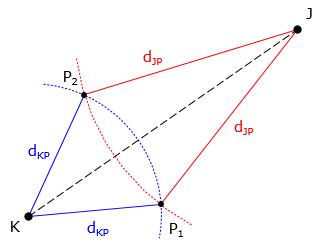
a. Distance-distance

The distance from each control point to the unknown point is known. Using control points as radius points and distances as radii, two arcs are extended to their intersections, Figure D-4.

Coordinates of the intersection points are determined by solving these equations in sequence:

Equation D-12 returns two East coordinates and Equation D-13, because it is in terms of East, returns the corresponding North coordinate of both intersection points. The correct point for the situation can then be selected from the two.

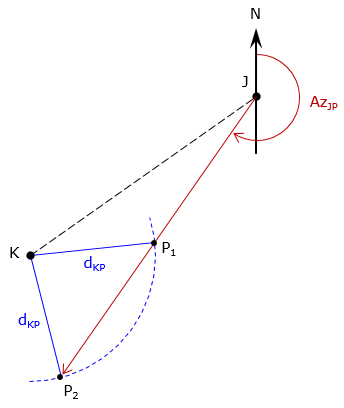
b. Direction-distance intersection

The direction from one known point and distance from a second is known.Treating the distance as a radius, an arc is extended to intersect the direction., Figure D-4.

To determine the coordinates of the intersection points:

	Equation D-14
	Equation D-15
		Equation D-16
		Equation D-17
		Equation D-18
		Equation D-19

Equation D-19 results in  are two possible distances, d_JP, from point J. Use each in the Forward Computation equations to determine the two coordinate pairs of point P, then select the correct one based on the situation.

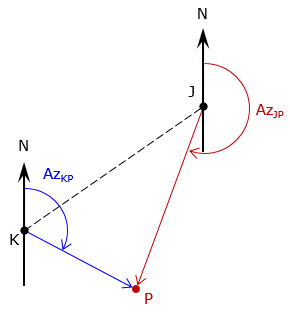
c. Direction-direction

Technically, because a distance is not part of the given information, the arc-based method isn't applicable for this type of intersection, Figure D-5. However, it is still possible to develop a general solution independent of triangle geometry.

This involves setting up Equations D-2 and D-3 from both ends of the base line. The North equations are set equal to each other, East equations equal to each other, then both simultaneously solved to determine the distance from a known point  to the intersection point. Because curves are not involved, there is just one intersection point.

To determine point P's coordinates from point J

The distance from point J is:

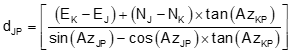Equation D-20

Forward Computation from point J

If a math check is desired

The distance from point K is

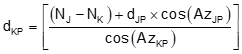Equation D-21

Forward Computation from point K