D. Arc-Based Intersections

1. Circle; Arc

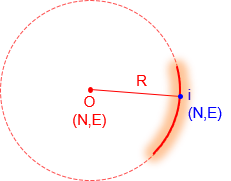
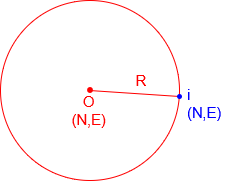
Figure D-1 is a diagram of a circle and Equation D-1 is its equation in terms of North and East coordinates.

Figure D-1 Circle

		Equation D-1
where:
O i R	radius point   point on circumference   radius

An arc is a portion of a circle, Figure D-2.

Generally we only need an arc long enough to meet an intersection condition. We'll cover other specific arc geometry in the Curvilinear Traverse chapter.

2. Solution logic

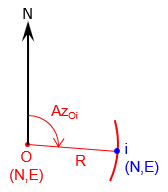
A radius is a distance, Figure D-3, so the Forward Computation equations of any point on an arc can be written as Equations D-2 and D-3.

	Equation D-2
	Equation D-3

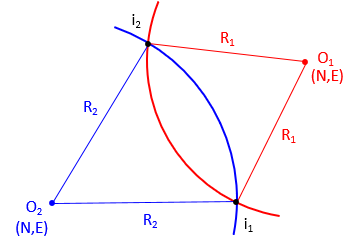
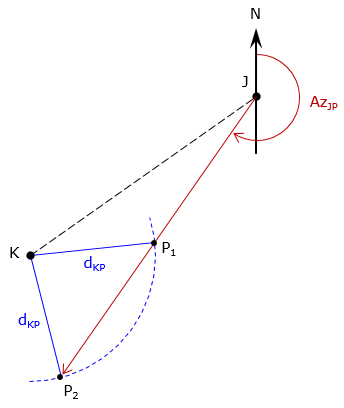
An arc-based intersection solution uses a radius for a distance. For example, Figure D-4 shows a distance-distance intersection using two known arc centers and two radii.

A direction-distance intersection is similar except only a single radius is used. Generally, coordinates of the intersection point are determined by simultaneous solution of Equations D-1, D-2, and D-3. A direction-direction intersection does not use distances so only Equations D-2 and D-3 are needed.

The disadvantages of the arc-based approach are:

• For someone new to COGO, solving intersections using triangles is simple and intuitive, using arcs is less so
• Coordinate solutions can involve numerous equations creating potential for computational errors
• Errors could also be easily introduced if coordinate orders in the equations are reversed

On the other hand:

• A triangle-based solution requires the user to decide what geometry to solve based on measurements provided and which position to solve; arc-based coordinate equations are general so they are just plug-and-chug
• Where there are two possible intersection solutions, both can be solved with little additional effort
• Arc-based solutions are computationally efficient, particularly for programming or spreadsheet applications
• Other types of problems, such as curve fitting, are easier to solve using arc-based methods

Because arcs are not linear, intersections involving them require solving a second degree polynomial, Equation D-4. A second degree polynomial has two possible answers which are determined using a quadratic solution, Equation D-5.

	Equation D-4
	Equation D-5

That means there are two intersection points when at least one measurement is an arc. We saw that in the triangle-based methods: distance-distance and direction-distance had two possible intersections, direction-direction did not.

Triangle-based and arc-based intersections have the same known positions and connecting measurement requirements. They differ only in how the data are manipulated to get the same results. To maintain consistency with previously described triangle-based solutions, points J and K will be used as known control points in the arc-based discussion.

3. Intersections

a. Distance-distance

The distance from each control point to the unknown point is known. Using control points as radius points and distances as radii, two arcs are extended to their intersections, Figure D-4.

Coordinates of the intersection points are determined by solving these equations in sequence:

Equation D-12 returns two East coordinates and Equation D-13, because it is in terms of East, returns the corresponding North coordinate of both intersection points. The correct point for the situation can then be selected from the two.

b. Direction-distance intersection

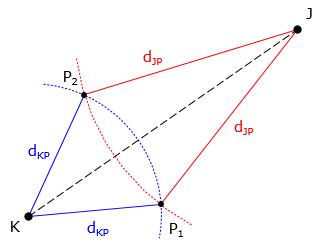
The direction from one known point and distance from a second is known.Treating the distance as a radius, an arc is extended to intersect the direction., Figure D-4.

To determine the coordinates of the intersection points:

	Equation D-14
	Equation D-15
		Equation D-16
		Equation D-17
		Equation D-18
		Equation D-19

Equation D-19 results in  are two possible distances, d_JP, from point J. Use each in the Forward Computation equations to determine the two coordinate pairs of point P, then select the correct one based on the situation.

c. Direction-direction

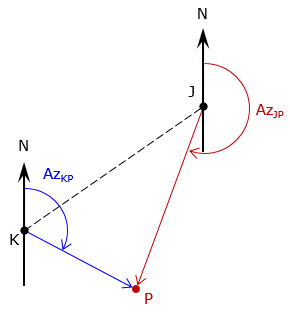
Technically, because a distance is not part of the given information, the arc-based method isn't applicable for this type of intersection, Figure D-5. However, it is still possible to develop a general solution independent of triangle geometry.

This involves setting up Equations D-2 and D-3 from both ends of the base line. The North equations are set equal to each other, East equations equal to each other, then both simultaneously solved to determine the distance from a known point  to the intersection point. Because curves are not involved, there is just one intersection point.

To determine point P's coordinates from point J

The distance from point J is:

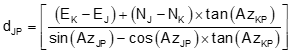Equation D-20

Forward Computation from point J

If a math check is desired

The distance from point K is

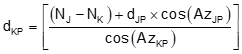Equation D-21

Forward Computation from point K

4. Comments

Limitations for the arc-based  method are the same as those of triangle-based. If the intersection type cannot be solved by one method, then the other method won't work either. For example, if the two directions are parallel, neither method will result in a direction-direction intersection. The only difference between the two methods is how the data are manipulated.