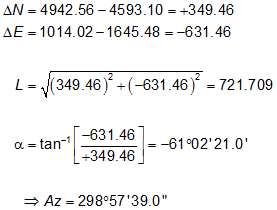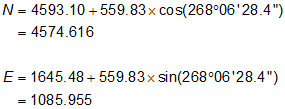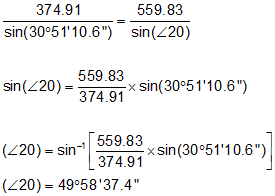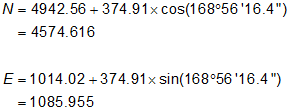E. Example Intersections
Two different intersection types are solved using triangle- and arc-based methods to demonstrate the different computation process. Additional decimal places will be carried in computations to minimize rounding errors.
1. Distance-distance
|
|
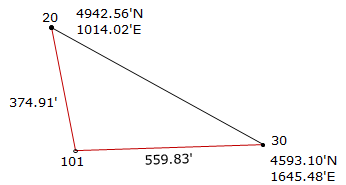
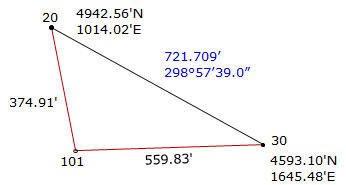
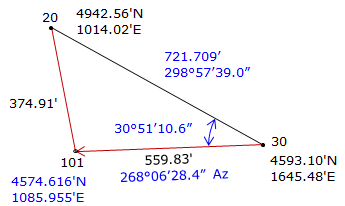
Given the information on the diagram, determine the coordinates of point 101.
|
|
Figure E-1 |
Step (1) For both methods is to inverse along the base line 30-20
|
|
 |
a. Triangle-based method
|
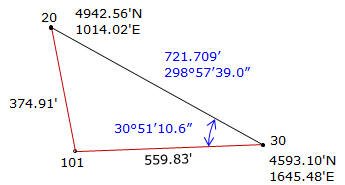
Step (2) Compute angle at 30 by Law of Cosines.
|
 |
|
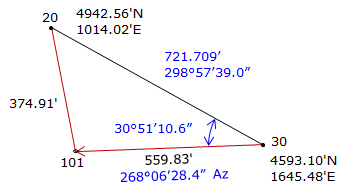
Step (3) Compute direction from 30 to 101.
|
 |
|
Step (4) Perform a forward computation from 30 to 101.
|
 |
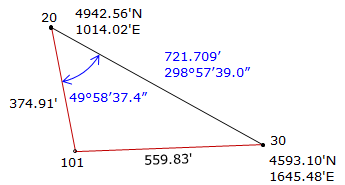
Math Check: Compute coordinates from 20.
|
Step (1) Compute angle at 20 by Law of Sines.
|
 |
|
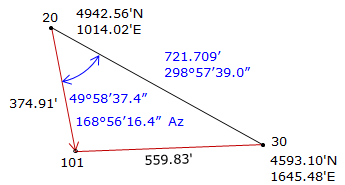
Step (2) Compute direction from 20 to 101.
|
 |
|
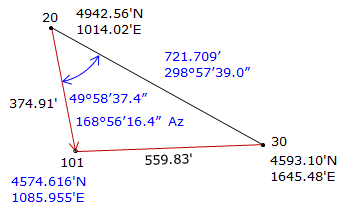
Step (3) Perform a forward computation from 20 to 101.
Both coordinates check. |
 |
b. Arc-based method
Step (2) Set up and solve Equations D-6 through D-9.
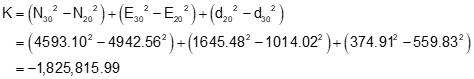
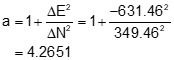

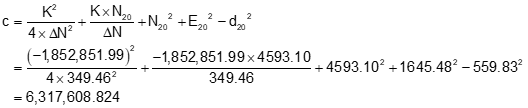
Step (3) Use Equations D-10 and D-11 to compute the two intersection points

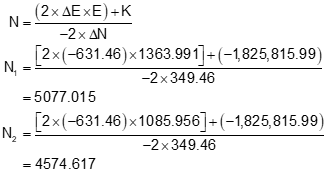
Step (4) Of the two, select the appropriate intersection point.
Point 101 is located southwest of the base line.
| Point | North | East | From base line |
| 1011 | 5077.015 | 1363.991 | north east |
| 1012 | 4574.617 | 1085.956 | south west |
The correct intersection point is 1012: (4754.617 ft N, 1085.956 ft E), same as the triangle-based solution.